题目内容
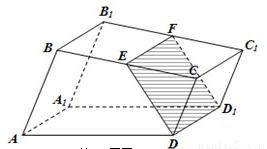
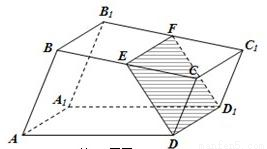
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为2、∠ADC=120°的菱形,Q是侧棱DD1(DD1> )延长线上的一点,过点Q、A1、C1作菱形截面QA1PC1交侧棱BB1于点P.设截面QA1PC1的面积为S1,四面体B1-A1C1P的三侧面△B1A1C1、△B1PC1、△B1A1P面积的和为S2,S=S1-S2.
)延长线上的一点,过点Q、A1、C1作菱形截面QA1PC1交侧棱BB1于点P.设截面QA1PC1的面积为S1,四面体B1-A1C1P的三侧面△B1A1C1、△B1PC1、△B1A1P面积的和为S2,S=S1-S2.(Ⅰ)证明:AC⊥QP;
(Ⅱ)当S取得最小值时,求cos∠A1QC1的值.

【答案】分析:(Ⅰ)要证明:AC⊥QP;只要证明AC垂直平面PCDQ即可.也就是证明AC垂直平面内的相交直线即可.
(Ⅱ)设O是A1C1与QP的交点,QD1=x、QO=y,则x2+1=y2,利用S=S1-S2.表示出面积S,当S取得最小值时,求出x的值,然后求cos∠A1QC1的值.
解答:解:(Ⅰ)连AC、BD,则AC⊥BD;
∵PB⊥底面ABCD,则AC⊥BP,∴AC⊥平面QPBD.
而QP?平面QPBD,∴AC⊥QP.(4分)
(Ⅱ)设O是A1C1与QP的交点,QD1=x、QO=y,则x2+1=y2,S=S1-S2
= =
= .(8分)
.(8分)
∵令 ,则
,则 ,
,
∴当 即
即 时,S取得最小值.(11分)
时,S取得最小值.(11分)
此时, ,由余弦定理有cos∠A1QC1=
,由余弦定理有cos∠A1QC1= .(13分)
.(13分)
点评:本题考查棱柱的结构特征,余弦定理,是中档题.
(Ⅱ)设O是A1C1与QP的交点,QD1=x、QO=y,则x2+1=y2,利用S=S1-S2.表示出面积S,当S取得最小值时,求出x的值,然后求cos∠A1QC1的值.
解答:解:(Ⅰ)连AC、BD,则AC⊥BD;
∵PB⊥底面ABCD,则AC⊥BP,∴AC⊥平面QPBD.
而QP?平面QPBD,∴AC⊥QP.(4分)
(Ⅱ)设O是A1C1与QP的交点,QD1=x、QO=y,则x2+1=y2,S=S1-S2
=
 =
= .(8分)
.(8分)∵令
 ,则
,则 ,
,∴当
 即
即 时,S取得最小值.(11分)
时,S取得最小值.(11分)此时,
 ,由余弦定理有cos∠A1QC1=
,由余弦定理有cos∠A1QC1= .(13分)
.(13分)点评:本题考查棱柱的结构特征,余弦定理,是中档题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
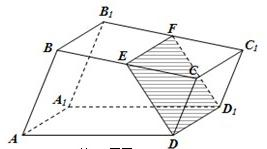 如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.
如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.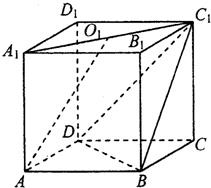 如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点.
如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点. 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: