题目内容
已知函数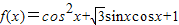 ,x∈R.
,x∈R.(1)求证f(x)的小正周期和最值;
(2)求这个函数的单调递增区间.
【答案】分析:(1)根据二倍解公式,我们易将函数的解析式化为正弦型函数;
(2)根据正弦函数的单调性,构造不等式-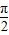 +2kπ≤2x+
+2kπ≤2x+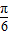 ≤
≤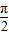 +2kπ,解不等式即可求出函数的单调增区间.
+2kπ,解不等式即可求出函数的单调增区间.
解答:解;(1)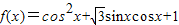 =
= cos2x+
cos2x+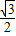 sin2x+
sin2x+ =sin(2x+
=sin(2x+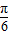 )+
)+
函数的周期T=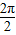 =π
=π
∵-1≤sin(2x+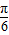 )≤1
)≤1
∴ ≤sin(2x+
≤sin(2x+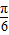 )+
)+ ≤
≤ 即
即 ≤f(x)≤
≤f(x)≤
(2)当-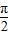 +2kπ≤2x+
+2kπ≤2x+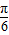 ≤
≤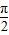 +2kπ⇒x∈[-
+2kπ⇒x∈[-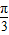 +kπ,
+kπ,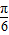 +kπ]为函数的单调增区间.
+kπ]为函数的单调增区间.
点评:本题考查的知识点是二倍角公式以及正弦函数的单调性,其中熟练函数的解析式化为正弦型函数是解答本题的关键.
(2)根据正弦函数的单调性,构造不等式-
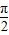 +2kπ≤2x+
+2kπ≤2x+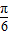 ≤
≤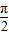 +2kπ,解不等式即可求出函数的单调增区间.
+2kπ,解不等式即可求出函数的单调增区间.解答:解;(1)
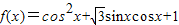 =
= cos2x+
cos2x+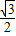 sin2x+
sin2x+ =sin(2x+
=sin(2x+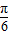 )+
)+
函数的周期T=
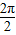 =π
=π∵-1≤sin(2x+
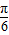 )≤1
)≤1∴
 ≤sin(2x+
≤sin(2x+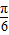 )+
)+ ≤
≤ 即
即 ≤f(x)≤
≤f(x)≤
(2)当-
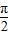 +2kπ≤2x+
+2kπ≤2x+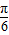 ≤
≤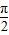 +2kπ⇒x∈[-
+2kπ⇒x∈[-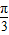 +kπ,
+kπ,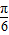 +kπ]为函数的单调增区间.
+kπ]为函数的单调增区间.点评:本题考查的知识点是二倍角公式以及正弦函数的单调性,其中熟练函数的解析式化为正弦型函数是解答本题的关键.

练习册系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.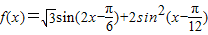 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.