题目内容

△ABC中，A，B，C所对的边为a，b，c．向量
m
=（
3
sin2x，1），
n
=（1，3+cos2x），设函数f（x）=
m
•
n
．
（1）讨论f（x）的单调区间；
（2）若2
AC
•
BC
=
2
ab，c=2
2
，f（A）=4，求b．
考点：平面向量的综合题
专题：综合题,平面向量及应用
分析：（1）向量
m
=（
3
sin2x，1），
n
=（1，3+cos2x），可得f（x）=
m
•
n
=
3
sin2x+3+cos2x=2sin（2x+
π
6
）+3，即可求出f（x）的单调区间；
（2）由f（A）=4，求出A，利用2
AC
•
BC
=
2
ab，求出C，可得B，再利用正弦定理即可求b．
解答： 解：（1）∵向量
m
=（
3
sin2x，1），
n
=（1，3+cos2x），
∴f（x）=
m
•
n
=
3
sin2x+3+cos2x=2sin（2x+
π
6
）+3，
由2x+
π
6
∈[2kπ-
π
2
，2kπ+
π
2
]，可得x∈[kπ-
π
3
，kπ+
π
6
]（k∈Z），即函数的单调增区间为[kπ-
π
3
，kπ+
π
6
]（k∈Z），
由2x+
π
6
∈[2kπ+
π
2
，2kπ+
3
2
π]，可得x∈[kπ+
π
6
，kπ+
2π
3
]（k∈Z），即函数的单调减区间为[kπ+
π
6
，kπ+
2π
3
]（k∈Z）；
（2）∵f（A）=4，
∴2sin（2A+
π
6
）+3=4，∴A=
π
3
，
∵2
AC
•
BC
=
2
ab，
∴2abcosC=
2
ab，
∴C=
π
4
，
∴B=
5π
12
，
∵c=2
2
，
∴b=
csinB
sinC
=
2
2
×(
2
2
×
3
2
+
2
2
×
1
2
)
2
2
=
6
+
2
．
点评：本题考查平面向量的数量积公式，考查三角函数的性质，考查正弦定理的运用，属于中档题．
练习册系列答案
相关题目
已知命题p：任意三角形的三个内角中至少有一个不大于60°，则命题p的否定是：
 
．
已知全集U=R，集合A={x|x-1≥0}，B={x|（x+1）（x-2）≤0}．
（1）求A∩B
（2）求∁U（A∪B）
下列说法正确的是（　　）
A、若a＞b＞0，a＞c则a2＞bc
B、若a＞b＞c则
a
c
＞
b
c
C、若a＞b，n∈N*则an＞bn
D、若a＞b＞0，则lna＜lnb
在数列{an}中，a1=2，an+1=2an2，求an．
在平面直角坐标系xOy中，圆C的方程为x2+y2-8x+15=0，若直线y=kx-2上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则k的取值范围是（　　）
A、[0，
4
3
]
B、（0，
4
3
）
C、[-
4
3
，
4
3
]
D、（0，
4
3
]
已知双曲线x2-
y2
b2
=1（b＞0）的离心率为
10
，则b=
 
．
函数f（x）=
x-1
x-2
的定义域为（　　）
A、（1，+∞）
B、[1，2）∪（2，+∞）
C、[1，2）
D、[1，+∞）
甲乙两名运动员在某项测试中的8次成绩如茎叶图所示，则甲运动员的极差与乙运动员的众数分别是（　　）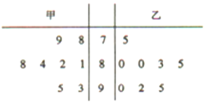
A、20、80
B、20、81
C、17、80
D、17、81

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网