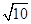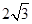题目内容
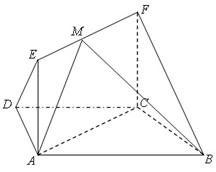
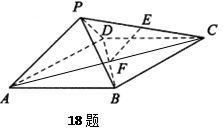
.(本题满分12分)如图,在梯形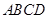 中,
中,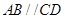 ,
,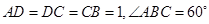 ,四边形
,四边形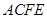 为矩形,平面
为矩形,平面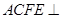 平面
平面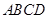 ,
,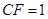 .
.
(I)求证: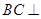 平面
平面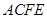 ;
;
(II)点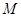 在线段
在线段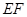 上运动,设平面
上运动,设平面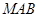 与平面
与平面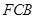 所成二面角的平面角为
所成二面角的平面角为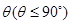 ,试求
,试求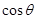 的取值范围.
的取值范围.
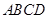 中,
中,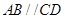 ,
,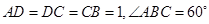 ,四边形
,四边形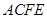 为矩形,平面
为矩形,平面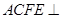 平面
平面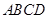 ,
,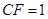 .
.(I)求证:
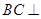 平面
平面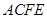 ;
;(II)点
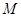 在线段
在线段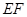 上运动,设平面
上运动,设平面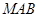 与平面
与平面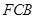 所成二面角的平面角为
所成二面角的平面角为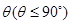 ,试求
,试求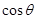 的取值范围.
的取值范围.
(I)证明:在梯形
 中,
中, ∵
 ,
, ,
,∠
 =
= ,∴
,∴ 
∴
 ∴
∴ 
∴
 ⊥
⊥
∵ 平面
 ⊥平面
⊥平面 ,平面
,平面 ∩平面
∩平面
 ,
,
 平面
平面
∴
 ⊥平面
⊥平面 …………………6分
…………………6分(II)由(I)可建立分别以直线
 为
为 的如图所示空间直角坐标系,令
的如图所示空间直角坐标系,令 ,则
,则 ,
,

∴

设
 为平面MAB的一个法向量,
为平面MAB的一个法向量,由
 得
得
取
 ,则
,则 ,…………8分
,…………8分∵
 是平面FCB的一个法向量
是平面FCB的一个法向量∴
 …10分
…10分∵
 ∴ 当
∴ 当 时,
时,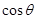 有最小值
有最小值 ,
,当
 时,
时,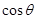 有最大值
有最大值 。 ∴
。 ∴  …………………12分
…………………12分略

练习册系列答案
相关题目
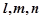 是三条不同的直线,
是三条不同的直线,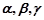 是三个不同的平面,则下列命题中为假命题的是
是三个不同的平面,则下列命题中为假命题的是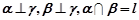 ,则
,则
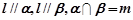 ,则
,则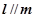
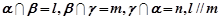 ,则
,则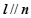
 ,则
,则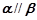 或
或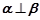
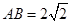 ,CC1=4,M是棱CC1上一点.
,CC1=4,M是棱CC1上一点.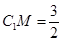 ,求二面角A-MB1-C的大小.
,求二面角A-MB1-C的大小.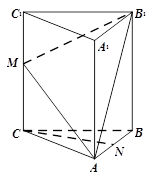
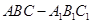 中,
中,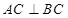 ,点
,点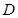 是
是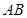 的中点.
的中点.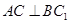 ;(2)
;(2)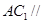 平面
平面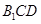 .
.
 中,
中,  ,
, 平面
平面 ,点
,点 是
是 的中点.
的中点. ;
; 平面
平面 ;
;
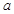 、
、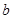 是两条不同直线,
是两条不同直线,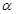 、
、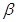 是两个不同平面,则下列四个命题:
是两个不同平面,则下列四个命题: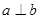 ,
,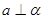 ,
,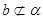 ,则
,则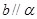 ;
;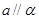 ,
,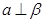 ,则
,则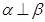 ;
;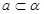 ;
;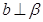 ,则
,则 中,
中, 分别是
分别是 的中点,
的中点, ,
, .
. //平面
//平面 ;
; 上是否存在点
上是否存在点 ,使直线
,使直线 与
与 垂直,
垂直,
 B
B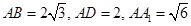 ,则点
,则点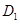 到直线AC的距离是
到直线AC的距离是