题目内容
已知集合A={x|-1≤x≤a,a>1且a∈R},B={y|y=2x-1,x∈A},C={z|z=x2,x∈A},是否存在a的值,使C⊆B?若存在,求出a的取值范围.若不存在,说明理由.
考点:元素与集合关系的判断
专题:集合
分析:由A化简B、C,假设C⊆B,得出
,求出a的取值范围即可.
|
解答:
解:∵A={x|-1≤x≤a,a>1且a∈R},
∴B={y|y=2x-1,x∈A}={y|-3≤y≤2a-1,a>1且a∈R},
C={z|z=x2,x∈A}={z|0≤z≤a2,a>1且a∈R},
∴若C⊆B,则
;
解得a∈∅,
∴不存在a,使C⊆B.
∴B={y|y=2x-1,x∈A}={y|-3≤y≤2a-1,a>1且a∈R},
C={z|z=x2,x∈A}={z|0≤z≤a2,a>1且a∈R},
∴若C⊆B,则
|
解得a∈∅,
∴不存在a,使C⊆B.
点评:本题考查了集合的应用问题,解题时应根据题意对集合进行化简,从而求出答案来,是基础题.

练习册系列答案
相关题目
方程2x+x=5的根所在的区间为( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
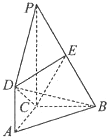 如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.
如图,DA⊥平面ABC,DA∥PC,∠ACB=90°,AC=AD=BC=1,PC=2,E为PB的中点.
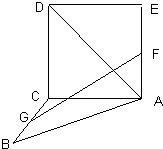 如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.
如图,正方形ACDE与等腰直角△ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F、G分别是线段AE、BC的中点.求AD与GF所成的角的余弦值.