题目内容
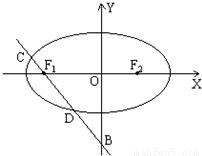
已知椭圆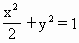 及点B(0,-2),过点B作直线m与椭圆交于C、D两点,
及点B(0,-2),过点B作直线m与椭圆交于C、D两点,
(1)试确定直线m的斜率k的取值范围.
(2)若直线m经过椭圆的左焦点F1,椭圆的右焦点为F2,求△CDF2的面积.
答案:
解析:
解析:
|
解:(1)设直线m的方程为y=kx-2,把它代入椭圆方程,得: (2)将左焦点坐标(-1,0)代入y=kx-2,得:k=-2.代入椭圆方程整理得:9x2+16x+6=0,解得:|x2-x1|= |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
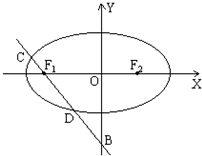 已知椭圆
已知椭圆 及点B(0,-2),过点B作直线l与椭圆交于C、D两点.
及点B(0,-2),过点B作直线l与椭圆交于C、D两点.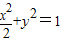 及点B(0,-2),过点B作直线l与椭圆交于C、D两点.
及点B(0,-2),过点B作直线l与椭圆交于C、D两点.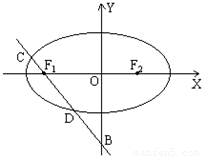
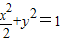 及点B(0,-2),过点B作直线l与椭圆交于C、D两点.
及点B(0,-2),过点B作直线l与椭圆交于C、D两点.