题目内容
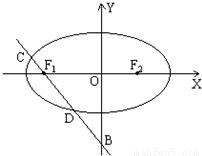
已知椭圆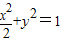 及点B(0,-2),过点B作直线l与椭圆交于C、D两点.
及点B(0,-2),过点B作直线l与椭圆交于C、D两点.(1)试确定直线l的斜率k的取值范围;
(2)若直线l经过椭圆的左焦点F1,椭圆的右焦点为F2,求△CDF2的面积.
【答案】分析:(1)设出直线l的方程,联立椭圆方程,利用直线和椭圆相交两个点,可得△>0,由此可求直线l的斜率k的取值范围;
(2)求出直线l的方程,点F2(1,0)到l的距离,计算|CD|,即可求得面积.
解答:解:(1)设直线l:y=kx-2,联立椭圆方程,消去y得:(1+2k2)x2-8kx+6=0(*)
由于直线和椭圆相交两个点,故△=8(2k2-3)>0,得: .
.
(2)直线l经过点B(0,-2)和F1(-1,0),所以l:2x+y+2=0
点F2(1,0)到l的距离
联立直线和椭圆方程得:9x2+16x+6=0,
∴
∴ .
.
点评:本题考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生的计算能力,属于中档题.
(2)求出直线l的方程,点F2(1,0)到l的距离,计算|CD|,即可求得面积.
解答:解:(1)设直线l:y=kx-2,联立椭圆方程,消去y得:(1+2k2)x2-8kx+6=0(*)
由于直线和椭圆相交两个点,故△=8(2k2-3)>0,得:
 .
.(2)直线l经过点B(0,-2)和F1(-1,0),所以l:2x+y+2=0
点F2(1,0)到l的距离

联立直线和椭圆方程得:9x2+16x+6=0,
∴

∴
 .
.点评:本题考查直线与椭圆的位置关系,考查三角形面积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
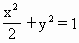 及点B(0,-2),过点B作直线m与椭圆交于C、D两点,
及点B(0,-2),过点B作直线m与椭圆交于C、D两点,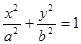 (a>b>0)
(a>b>0)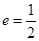 ,一条准线方程为x=4 时,求椭圆方程;
,一条准线方程为x=4 时,求椭圆方程;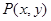 是椭圆上一点,在(1)的条件下,求
是椭圆上一点,在(1)的条件下,求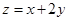 的最大值及相应的P点坐标。
的最大值及相应的P点坐标。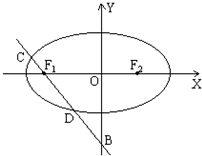 已知椭圆
已知椭圆 及点B(0,-2),过点B作直线l与椭圆交于C、D两点.
及点B(0,-2),过点B作直线l与椭圆交于C、D两点.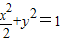 及点B(0,-2),过点B作直线l与椭圆交于C、D两点.
及点B(0,-2),过点B作直线l与椭圆交于C、D两点.