题目内容
已知椭圆过点P(-3,
),Q(2,
).
(1)求椭圆的方程;
(2)若A(0,4),B是椭圆上的任一点,求|AB|的最大值及此时B的坐标.
| ||
| 2 |
| 3 |
(1)求椭圆的方程;
(2)若A(0,4),B是椭圆上的任一点,求|AB|的最大值及此时B的坐标.
分析:(1)设出椭圆方程mx2+ny2=1(m>0,n>0),把点的坐标代入椭圆方程后联立方程组求解m,n的值,则椭圆的方程可求;
(2)化椭圆的普通方程为参数方程,得到B点的坐标由两点间的距离公式写出|AB|,利用配方法即可求出|AB|的最大值,且同时求出B的坐标.
(2)化椭圆的普通方程为参数方程,得到B点的坐标由两点间的距离公式写出|AB|,利用配方法即可求出|AB|的最大值,且同时求出B的坐标.
解答:解:(1)设椭圆方程为mx2+ny2=1(m>0,n>0).
因为椭圆过点P(-3,
),Q(2,
),
所以
,解得
.
所以椭圆方程为
+
=1;
(2)由椭圆方程为
+
=1,
可知A(0,4)在椭圆外部,
椭圆的参数方程
,
因为B为椭圆上的任一点,设B(4cosθ,2sinθ),
所以|AB|=
=
=
=
=
.
所以当sinθ=-
时,|AB|的最大值为
.
此时cosθ=-
.
则B(-
,-
).
因为椭圆过点P(-3,
| ||
| 2 |
| 3 |
所以
|
|
所以椭圆方程为
| x2 |
| 16 |
| y2 |
| 4 |
(2)由椭圆方程为
| x2 |
| 16 |
| y2 |
| 4 |
可知A(0,4)在椭圆外部,
椭圆的参数方程
|
因为B为椭圆上的任一点,设B(4cosθ,2sinθ),
所以|AB|=
| 16cos2θ+(2sinθ-4)2 |
=
| 16cos2θ+4sin2θ-16sinθ+16 |
=
| 12cos2θ-16sinθ+20 |
=
| -12sin2θ-16sinθ+32 |
=
-12(sinθ+
|
所以当sinθ=-
| 2 |
| 3 |
4
| ||
| 3 |
此时cosθ=-
| ||
| 3 |
则B(-
4
| ||
| 3 |
| 4 |
| 3 |
点评:本题考查了椭圆的方程,考查了椭圆的参数方程,训练了两点间的距离公式,训练了利用配方法求最值,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
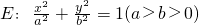 过点P(3,1),其左、右焦点分别为F1,F2,且
过点P(3,1),其左、右焦点分别为F1,F2,且 ,则椭圆E的离心率是________.
,则椭圆E的离心率是________. ),Q(2,
),Q(2, ).
). 过点P(3,1),其左、右焦点分别为F1,F2,且
过点P(3,1),其左、右焦点分别为F1,F2,且 ,则椭圆E的离心率是 .
,则椭圆E的离心率是 .