题目内容
已知 是正数,
是正数, ,
, ,
, .
.
(Ⅰ)若 成等差数列,比较
成等差数列,比较 与
与 的大小;
的大小;
(Ⅱ)若 ,则
,则 三个数中,哪个数最大,请说明理由;
三个数中,哪个数最大,请说明理由;
(Ⅲ)若 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整数部分分别是
的整数部分分别是

 求所有
求所有 的值.
的值.
(Ⅰ)
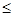
 ;(Ⅱ)
;(Ⅱ)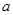 最大;(Ⅲ)
最大;(Ⅲ)
解析试题分析:(Ⅰ)用作差法比较大小,用对数的运算法则化简后与0作比较。此时只需对数的真数与1作比较即可,根据单调性比得出对数和0的大小,从而得出 与
与 的大小。(Ⅱ)运用对数的运算法则将不等式化简,再根据对数的单调性得真数的不等式,即关于a,b,c的不等式通过整理即可比较出三者中谁最大。(Ⅲ)由已知可得
的大小。(Ⅱ)运用对数的运算法则将不等式化简,再根据对数的单调性得真数的不等式,即关于a,b,c的不等式通过整理即可比较出三者中谁最大。(Ⅲ)由已知可得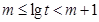 ,根据对数的运算法则可得
,根据对数的运算法则可得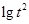 的范围,得到其整数部分,根据已知其整数部分可列式求得
的范围,得到其整数部分,根据已知其整数部分可列式求得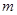 的可能取值。然后分情况讨论,解对数不等式可求得
的可能取值。然后分情况讨论,解对数不等式可求得 的值。
的值。
试题解析:解:(Ⅰ)由已知得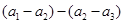 =
=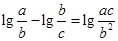 .
.
因为 成等差数列,所以
成等差数列,所以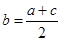 ,
,
则
 ,
,
因为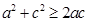 ,所以
,所以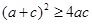 ,即
,即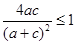 ,
,
则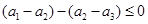 ,即
,即
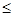
 ,当且仅当
,当且仅当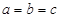 时等号成立.
时等号成立.
4分
(Ⅱ)解法1:令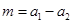 ,
,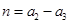 ,
,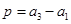 ,
,
依题意,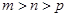 且
且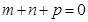 ,所以
,所以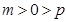 .
.
故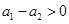 ,即
,即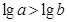 ;且
;且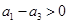 ,即
,即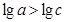 .
.
所以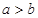 且
且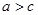 .
.
故 三个数中,
三个数中,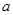 最大.
最大.
解法2:依题意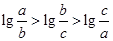 ,即
,即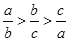 .
.
因为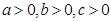 ,所以
,所以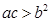 ,
,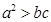 ,
,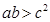 .
.
于是, ,
,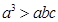 ,
,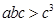 ,
,
所以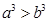 ,
,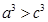 .
.
因为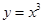 在
在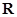 上为增函数,所以
上为增函数,所以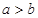 且
且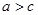 .
.
故 三个数中,
三个数中,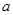 最大. 8分
最大. 8分
(Ⅲ)依题意, ,
,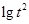 ,
,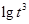 的整数部分分别是
的整数部分分别是

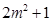 ,则
,则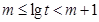 ,
,
所以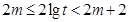 .
.
又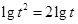 ,则
,则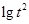 的整数部分是
的整数部分是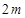 或
或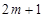 .
.
当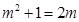 时,
时,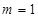 ;
;
当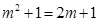 时,
时,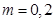 .
.
当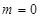 时,
时, ,
,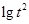 ,
,
练习册系列答案
相关题目
某跨国饮料公司对全世界所有人均GDP(即人均纯收入)在0.5—8千美元的地区销售,该公司M饮料的销售情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数中(x表示人均GDP,单位:千美元;y表示年人均M饮料的销量,单位:升),用哪个来描述人均,饮料销量与地区的人均GDP的关系更合适?说明理由.
A.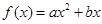 | B.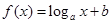 | C.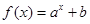 | D.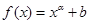 |
(3)因为M饮料在N国被检测出杀虫剂的含量超标,受此事件影响,M饮料在人均GDP不高于3千美元的地区销量下降5%,不低于6千美元的地区销量下降5%,其他地区的销量下降10%,根据(2)所求出的模拟函数,求在各个地区中,年人均M饮料的销量最多为多少?
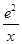 (x>0).
(x>0).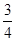 是省外游客,其余是省内游客.在省外游客中有
是省外游客,其余是省内游客.在省外游客中有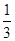 持金卡,在省内游客中有
持金卡,在省内游客中有 持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;
持银卡.(1)在该团中随机采访2名游客,求恰有1人持银卡的概率;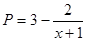 (其中
(其中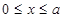 ,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为
,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为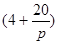 万元/万件.
万元/万件.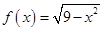 的定义域为集合
的定义域为集合 .
. 的定义域也为集合
的定义域也为集合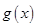 的值域为
的值域为 ,求
,求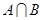 ;
;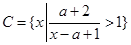 ,若
,若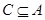 ,求实数
,求实数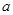 的取值范围.
的取值范围.
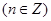 满足
满足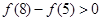 .
. 的解析式;
的解析式;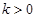 ,使
,使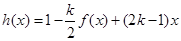 在区间
在区间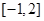 上的值域为
上的值域为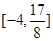 ?若存在,求出
?若存在,求出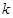 ;若不存在,请说明理由.
;若不存在,请说明理由. ,
,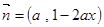 ,其中
,其中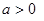 .函数
.函数 在区间
在区间 上有最大值为4,设
上有最大值为4,设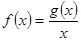 .
.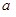 的值;
的值;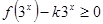 在
在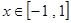 上恒成立,求实数
上恒成立,求实数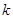 的取值范围.
的取值范围.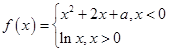 ,其中
,其中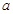 是实数,设
是实数,设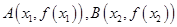 为该函数的图象上的两点,且
为该函数的图象上的两点,且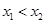 .
. 的单调区间;
的单调区间;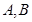 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求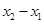 的最小值;
的最小值;