题目内容
已知函数
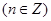 满足
满足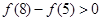 .
.
(1)求 的解析式;
的解析式;
(2)对于(1)中得到的函数 ,试判断是否存在
,试判断是否存在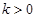 ,使
,使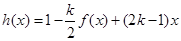 在区间
在区间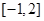 上的值域为
上的值域为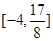 ?若存在,求出
?若存在,求出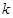 ;若不存在,请说明理由.
;若不存在,请说明理由.
(1)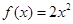 ;(2)存在
;(2)存在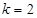 满足条件
满足条件
解析试题分析:(1)由条件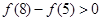 结合幂函数的图像与性质可知
结合幂函数的图像与性质可知 在第一象限单调递增,从而可得
在第一象限单调递增,从而可得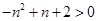 ,解出
,解出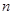 的整数解即可得到函数的解析式;(2)先假设存在
的整数解即可得到函数的解析式;(2)先假设存在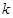 的值满足题意,然后根据二次函数取得最值的位置:区间的端点与对称轴的位置,进行确定
的值满足题意,然后根据二次函数取得最值的位置:区间的端点与对称轴的位置,进行确定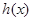 在什么位置取得最大值与最小值,最后根据题目所给的最值即可得到参数
在什么位置取得最大值与最小值,最后根据题目所给的最值即可得到参数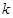 的值.
的值.
试题解析:(1)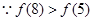 ,由幂函数的性质可知,
,由幂函数的性质可知, 在第一象限为增函数
在第一象限为增函数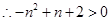 ,得
,得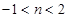 ,又由
,又由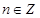 ,所以
,所以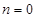 或
或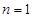 5分
5分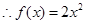 6分
6分
(2)假设存在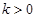 满足条件,由已知
满足条件,由已知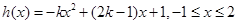 8分
8分
而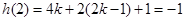 9分
9分
所以两个最值点只能在端点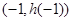 和顶点
和顶点 处取得
处取得
而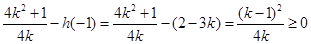 11分
11分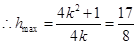 且
且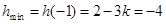
解得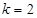 13分
13分 存在
存在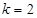 满足条件 14分.
满足条件 14分.
考点:幂函数及二次函数的单调性与最值.

练习册系列答案
相关题目
 ,其中
,其中 为常数.
为常数.  在区间
在区间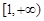 上单调,求
上单调,求 的取值范围;
的取值范围;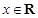 ,都有
,都有 成立,且函数
成立,且函数 的图象经过点
的图象经过点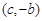 ,
, 是正数,
是正数, ,
, ,
, .
. 与
与 的大小;
的大小; ,则
,则 ,
, ,
, (
( ),且
),且 ,
, ,
, 的整数部分分别是
的整数部分分别是

 求所有
求所有 的值.
的值.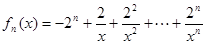 .
.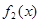 在
在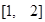 上的值域;
上的值域;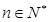 ,在
,在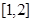 上存在唯一的
上存在唯一的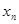 ,使得
,使得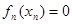 ;
; 的值.
的值. R.
R.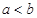 ,比较
,比较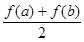 与
与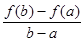 的大小并说明理由。
的大小并说明理由。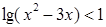
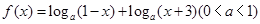
 的定义域;
的定义域; 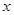 (百台),其总成本为
(百台),其总成本为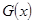 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入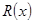 (万元)满足
(万元)满足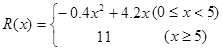 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题: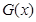 和利润函数
和利润函数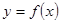 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);