题目内容
如图,已知直线l:y=2x-4交抛物线y2=4x于A,B两点,试在抛物线AOB这段曲线上求一点P,使△PAB的面积最大,并求出这个最大面积.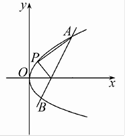
P( ,1),△PAB的面积最大值为
,1),△PAB的面积最大值为
解析试题分析:由 解得A(4,4)、B(1,-2),知|AB|=3
解得A(4,4)、B(1,-2),知|AB|=3 .设P(x0,y0)为抛物线AOB这段曲线上一点,d为P点到直线AB的距离,则
.设P(x0,y0)为抛物线AOB这段曲线上一点,d为P点到直线AB的距离,则
 ,∵-2<y0<4,∴(y0-1)2-9<0.
,∵-2<y0<4,∴(y0-1)2-9<0.
∴d= [9-(y0-1)2].从而当y0=1时,max=
[9-(y0-1)2].从而当y0=1时,max= ,Smax=
,Smax= .
.
因此,点P在( ,1)处时,△PAB的面积取得最大值,最大值为
,1)处时,△PAB的面积取得最大值,最大值为 .
.
考点:直线和抛物线位置关系及点到直线距离
点评:P点还可用与已知直线平行的直线与抛物线相切确定

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
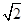 )在椭圆上,。
)在椭圆上,。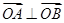 ,求△OAB的面积的取值范围。
,求△OAB的面积的取值范围。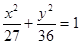 有相同焦点,且经过点
有相同焦点,且经过点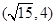 ,
,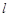 过点(0,3)且与抛物线y2=2x只有一个公共点,求该直线方程.
过点(0,3)且与抛物线y2=2x只有一个公共点,求该直线方程.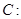
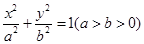 的离心率为
的离心率为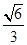 ,椭圆短轴的一个端点与两个焦
,椭圆短轴的一个端点与两个焦 的方程;
的方程;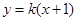 与椭圆
与椭圆 、
、 两点. ①若线段
两点. ①若线段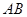 中点的
中点的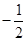 ,求斜率
,求斜率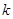 的值;②若点
的值;②若点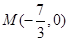 ,求证:
,求证: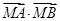 为定值.
为定值. 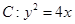 ,
,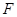 是抛物线
是抛物线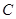 的焦点,过点
的焦点,过点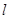 与
与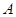 、
、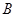 两点,
两点,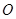 为坐标原点.
为坐标原点. 为直径的圆的方程;
为直径的圆的方程;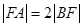 ,求直线
,求直线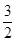 ),两个焦点为(-1,0)(1,0)?
),两个焦点为(-1,0)(1,0)?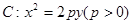 和点
和点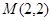 ,.斜率为
,.斜率为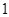 的直线与抛物线
的直线与抛物线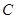 相交不同的两个点
相交不同的两个点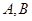 .若点
.若点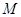 恰好为
恰好为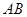 的中点.
的中点.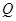 ,使得经过点
,使得经过点 的圆和抛物线
的圆和抛物线