Question

3．设实数x，y满足$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-5≥0}\\{y-2≤0}\end{array}\right.$，则μ=$\frac{{x}^{2}+{y}^{2}}{xy}$的取值范围[2，$\frac{10}{3}$]；若ax+y$≥\frac{{y}^{2}}{x}$恒成立，则实数a的取值范围a≥2．

Answer 1

分析 先根据约束条件画出可行域，设z₁=$\frac{y}{x}$，再利用z₁的几何意义求最值得出$\frac{y}{x}$的取值范围，最后将μ=$\frac{{x}^{2}+{y}^{2}}{xy}$表示为$\frac{y}{x}$的函数，即可解出μ=$\frac{{x}^{2}+{y}^{2}}{xy}$的取值范围．若ax+y$≥\frac{{y}^{2}}{x}$恒成立，则a≥t²-t，求出右边的最大值，即可求得实数a的取值范围

解答 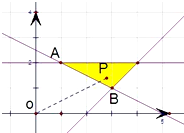解：在平面直角坐标系上作出可行域后，
原点与可行域内任意一点的连线的斜率即$\frac{y}{x}$，
易求当连线过点A（1，2）时最大，最大值为2；当连线过点B（3，1）时最小，最小值为$\frac{1}{3}$
∴$\frac{y}{x}$∈[$\frac{1}{3}$，2]，
设t=$\frac{y}{x}$∈[$\frac{1}{3}$，2]，
μ=$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{y}{x}$+$\frac{x}{y}$=t+$\frac{1}{t}$∈[2，$\frac{10}{3}$]；
若ax+y$≥\frac{{y}^{2}}{x}$恒成立，则a≥t²-t，
∵t∈[$\frac{1}{3}$，2]，
∴t²-t=（t-$\frac{1}{2}$）²-$\frac{1}{4}$$∈[-\frac{1}{4}，2]$，
∴a≥2．
故答案为：[2，$\frac{10}{3}$]；a≥2．

点评 本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．