题目内容
无穷等比数列{an}中,公比为q,且所有项的和为 ,则a1的范围是________.
,则a1的范围是________.
(0, )∪(
)∪( ,
, )
)
分析:根据数列为无穷等比数列,且所有项的和为 ,得到极限存在,即公比q大于等于-1小于等于1,且不为0,当官公比q等于1时,数列为常数列,利用首项a1表示出数列的前n项的和,解出a1,当n趋于无穷大时a1趋于0,得到a1大于0,当q大于等于-1小于1时,利用等比数列的前n项和公式表示出sn,当n趋于无穷大时,qn趋于0,得到sn=
,得到极限存在,即公比q大于等于-1小于等于1,且不为0,当官公比q等于1时,数列为常数列,利用首项a1表示出数列的前n项的和,解出a1,当n趋于无穷大时a1趋于0,得到a1大于0,当q大于等于-1小于1时,利用等比数列的前n项和公式表示出sn,当n趋于无穷大时,qn趋于0,得到sn= =
= ,解出a1,根据当q=-1时,a1取得最大值,即可解出a1的取值范围,同时因为公比q不为0,得到a1不等于
,解出a1,根据当q=-1时,a1取得最大值,即可解出a1的取值范围,同时因为公比q不为0,得到a1不等于 ,综上,写出a1的取值范围即可.
,综上,写出a1的取值范围即可.
解答:因为数列{an}为无穷等比数列,且其所有项的和为 ,即其极限存在,
,即其极限存在,
故可知|q|≤1且q≠0,即-1≤q≤1且q≠0,
当q=1时,无穷等比数列{an}为常数列,设sn为其所有项之和,则sn=na1= ,
,
即a1=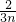 ,当n→+∞时,a1→0,即a1>0;
,当n→+∞时,a1→0,即a1>0;
当-1≤q<1时,sn=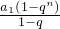 ,当n→+∞时,qn→0,于是有sn=
,当n→+∞时,qn→0,于是有sn= =
= ,
,
即a1= (1-q),当q=-1时,a1最大,所以得到0<a1≤
(1-q),当q=-1时,a1最大,所以得到0<a1≤ ,
,
又q≠0,得到a1≠ ,
,
综上,a1的范围是(0, )∪(
)∪( ,
, ).
).
故答案为:(0, )∪(
)∪( ,
, )
)
点评:此题考查学生灵活运用等比数列的前n项和公式化简求值,要求学生会利用极限思想解决实际问题,是一道中档题.学生求a1范围的时候注意q不为0这个条件得到a1≠ .
.
 )∪(
)∪( ,
, )
)分析:根据数列为无穷等比数列,且所有项的和为
 ,得到极限存在,即公比q大于等于-1小于等于1,且不为0,当官公比q等于1时,数列为常数列,利用首项a1表示出数列的前n项的和,解出a1,当n趋于无穷大时a1趋于0,得到a1大于0,当q大于等于-1小于1时,利用等比数列的前n项和公式表示出sn,当n趋于无穷大时,qn趋于0,得到sn=
,得到极限存在,即公比q大于等于-1小于等于1,且不为0,当官公比q等于1时,数列为常数列,利用首项a1表示出数列的前n项的和,解出a1,当n趋于无穷大时a1趋于0,得到a1大于0,当q大于等于-1小于1时,利用等比数列的前n项和公式表示出sn,当n趋于无穷大时,qn趋于0,得到sn= =
= ,解出a1,根据当q=-1时,a1取得最大值,即可解出a1的取值范围,同时因为公比q不为0,得到a1不等于
,解出a1,根据当q=-1时,a1取得最大值,即可解出a1的取值范围,同时因为公比q不为0,得到a1不等于 ,综上,写出a1的取值范围即可.
,综上,写出a1的取值范围即可.解答:因为数列{an}为无穷等比数列,且其所有项的和为
 ,即其极限存在,
,即其极限存在,故可知|q|≤1且q≠0,即-1≤q≤1且q≠0,
当q=1时,无穷等比数列{an}为常数列,设sn为其所有项之和,则sn=na1=
 ,
,即a1=
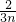 ,当n→+∞时,a1→0,即a1>0;
,当n→+∞时,a1→0,即a1>0;当-1≤q<1时,sn=
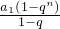 ,当n→+∞时,qn→0,于是有sn=
,当n→+∞时,qn→0,于是有sn= =
= ,
,即a1=
 (1-q),当q=-1时,a1最大,所以得到0<a1≤
(1-q),当q=-1时,a1最大,所以得到0<a1≤ ,
,又q≠0,得到a1≠
 ,
,综上,a1的范围是(0,
 )∪(
)∪( ,
, ).
).故答案为:(0,
 )∪(
)∪( ,
, )
)点评:此题考查学生灵活运用等比数列的前n项和公式化简求值,要求学生会利用极限思想解决实际问题,是一道中档题.学生求a1范围的时候注意q不为0这个条件得到a1≠
 .
. 
练习册系列答案
相关题目