题目内容
△ABC中，如果lgcosA=lgsinC-lgsinB=-lg2，则△ABC的形状是
- A.等边三角形
- B.直角三角形
- C.等腰三角形
- D.等腰直角三角形
B
分析：由lgcosA=lgsinC-lgsinB=-lg2可得lgcosA=lg
=-lg2可得
结合0＜A＜π 可求
，
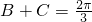，代入sinC=
sinB=
=
，从而可求C，B，进而可判断
解答：由lgcosA=lgsinC-lgsinB=-lg2可得lgcosA=lg=-lg2
∴
∵0＜A＜π∴，
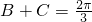
∴sinC=sinB==
∴tanC=
，C=
，B=
故选：B
点评：本题主要考查了对数的运算性质的应用，两角差的正弦公式的应用，解题的关键是灵活利用基本公式．
分析：由lgcosA=lgsinC-lgsinB=-lg2可得lgcosA=lg
=-lg2可得结合0＜A＜π 可求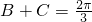，，代入sinC=sinB==，从而可求C，B，进而可判断解答：由lgcosA=lgsinC-lgsinB=-lg2可得lgcosA=lg
=-lg2∴
∵0＜A＜π∴
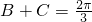
，∴sinC=
sinB==∴tanC=
，C=，B=故选：B
点评：本题主要考查了对数的运算性质的应用，两角差的正弦公式的应用，解题的关键是灵活利用基本公式．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
，且B为锐角，试判断该三角形的形状．
，并且B为锐角，则△ABC的形状是（ ）
，且B为锐角，判断此三角形的形状.
，且B为锐角，试判断此三角形的形状.
，并且B为锐角，则△ABC的形状是（ ）