Question

在△ABC中，如果lga-lgc＝lgsinB＝-lg，且B为锐角，判断此三角形的形状.

 

Answer 1

【答案】

三角形是等腰直角三角形.

【解析】

试题分析： 解：由lga-lgc＝lgsinB＝-lg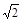，得 sinB＝，

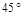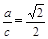又B为锐角，∴ B＝，又  得，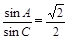

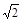∴ sinC＝2sinA＝2sin(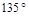-C)，   ∴ sinC＝sinC+cosC，

∴ cosC＝0  即C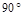＝，  故此三角形是等腰直角三角形.

考点 :本题主要考查正弦定理的应用，对数运算法则。

点评：涉及三角形形状判断问题，一般有两种思路，一是转化为边的问题，应用余弦定理，二是转化为角的问题，应用正弦定理，应根据题意灵活选择。