题目内容
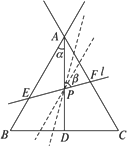
在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当
>β>α时,平面π与圆锥面的交线为______.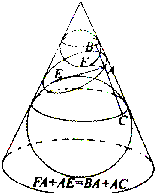
| π |
| 2 |

不同倾角的截面截割圆锥,无论是两个对顶的圆锥,还是一个单个的圆锥,都有下面的关系:
(1)β>α,平面π与圆锥的交线为椭圆;
(2)β=α,平面π与圆锥的交线为抛物线;
(3)β<α,平面π与圆锥的交线为双曲线.
由于题中条件:
>β>α,
故平面π与圆锥面的交线为 椭圆.
故答案为:椭圆.
(1)β>α,平面π与圆锥的交线为椭圆;
(2)β=α,平面π与圆锥的交线为抛物线;
(3)β<α,平面π与圆锥的交线为双曲线.
由于题中条件:
| π |
| 2 |
故平面π与圆锥面的交线为 椭圆.
故答案为:椭圆.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
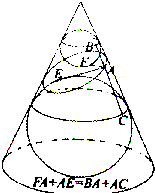 在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当
在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当