Question

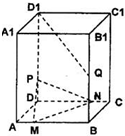已知正四棱柱ABCD-A₁B₁C₁D₁的底面边长为4，侧棱长为6，Q为BB₁的中点，P∈DD₁，M∈AB，N∈CD且AM=1，DN=3，（I）若PD=

3

2

，证明：（I）D₁Q∥面PMN；
（II）若P为DD₁的中点，求面PMN与面AA₁D₁D所成二面角的大小；
（III）在（II）的条件下，求点Q到面PMN的距离．

Answer 1

分析：（I）设DD₁中点为E，连接BE，连接BD交MN于R．根据棱柱的性质，可以证出四边形QBED₁是平行四边形，得到D₁Q∥BE；用△DRN与△BRM全等，可以证出R是BD中点，利用三角形BDE的中位线，证出PR∥BE，从而得到PR∥D₁Q．最后用线面平行的判定定理，可证出D₁Q∥面PMN；
（II）分别以DA、DC、DD₁为x轴、y轴、z轴，建立如图坐标系，然后求出点P、M、N的坐标，可得向量

PM

、

MN

的坐标，然后再用向量数量积的方法，通过解方程组得到平面PMN的一个法向量

n1

=(1，2，2)，再找到平面AA₁D₁D一个的法向量

n2

=(0，1，0)，最后求出向量

n1

，

n2

的夹角，从而得到面PMN与面AA₁D₁D所成二面角的大小；
（III）在（II）的坐标系下，求出由点Q指向面PMN内点P的向量

QP

的坐标，结合面PMN的一个法向量

n1

=(1，2，2)，利用空间点到平面距离的公式，可求得Q到面PMN的距离．

解答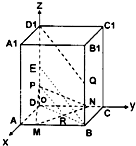：解：（I）设DD₁中点为E，连接BE，连接BD交MN于R
∵正四棱柱ABCD-A₁B₁C₁D₁中，BB₁∥DD₁且BB₁=DD₁
∴D₁E∥BQ且D₁E=BQ
∴四边形QBED₁是平行四边形，可得D₁Q∥BE
在正方形ABCD中，BM∥DN且BM=DN=3
∴△DRN≌△BRM⇒DR=BR
∵PD=

3

2

=

1

2

DE
∴△DBE中，PR是中位线
∴PR∥BE⇒PR∥D₁Q
∵PR?平面PMN，D₁Q?平面PMN，
∴D₁Q∥面PMN；
（II）分别以DA、DC、DD₁为x轴、y轴、z轴，建立如图坐标系，
则P（0，0，3），M（4，1，0），N（0，3，0）
设平面PMN的法向量为

n1

=(x，y，z)，根据垂直向量的数量积为零，
得

n1 • PM =4x+y-3z=0 n1 • MN =-4x+2y=0

，取x=1，得y=z=2
∴

n1

=(1，2，2)
∵平面AA₁D₁D的法向量为

n2

=(0，1，0)
∴cos＜

n1

，

n2

＞=

n1 • n2

|n1| |n2|

=

1×0+2×1+2×0

12+22+22 •1

=

2

3

∴面PMN与面AA₁D₁D所成二面角的大小为arccos

2

3

（III）∵P（0，0，3），Q（4，4，3）
∴

QP

=(-4，-4，0)
根据点到平面距离公式，得Q到面PMN的距离为
d=

|QP • n1|

|n1|

=|

-4×1+(-4)×2+0×2

3

| =3
所以点Q到面PMN的距离为3．

点评：本题以求二面角的大小和求点到平面的距离为例，着重考查了线面平行的证明、空间平面与平面所成角的公式和空间点到平面距离公式等知识点，属于难题．