题目内容
判断函数y=x+ 在在(0,2]、[2,+∝)上的单调性.
在在(0,2]、[2,+∝)上的单调性.
解:设0<x1<x2,
则 y1-y2
=(x1+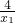 )-(x2+
)-(x2+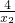 )
)
=(x1-x2)+(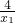 -
-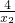 )
)
=(x1-x2)+[ ]
]
=(x1-x2)[1-(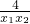 )]
)]
(1)假如0<x1<x2<2,则 0<x1x2<4,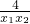 >1,1-
>1,1-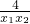 <0,
<0,
x1-x2<0,
所以,y1-y2>0,y1>y2,函数单调递减
(2)假如2<x1<x2,则 x1x2>4,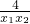 <1,1-
<1,1-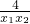 >0,
>0,
又x1-x2<0,
所以,y1-y2<0,y1<y2,函数单调递增
所以函数在(0,2)内单调递减;在[2,+∞)内单调递增.
分析:设0<x1<x2,化简 y1-y2 的解析式到因式乘积的形式,假如0<x1<x2<2,
判断y1-y2的符号,得出结论; 假如2<x1<x2,判断y1-y2 的符号,得出结论.
点评:本题考查利用函数的单调性的定义证明函数的单调性,体现分类讨论的数学思想.
则 y1-y2
=(x1+
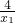 )-(x2+
)-(x2+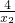 )
)=(x1-x2)+(
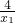 -
-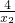 )
)=(x1-x2)+[
 ]
]=(x1-x2)[1-(
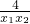 )]
)](1)假如0<x1<x2<2,则 0<x1x2<4,
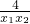 >1,1-
>1,1-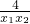 <0,
<0,x1-x2<0,
所以,y1-y2>0,y1>y2,函数单调递减
(2)假如2<x1<x2,则 x1x2>4,
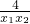 <1,1-
<1,1-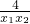 >0,
>0,又x1-x2<0,
所以,y1-y2<0,y1<y2,函数单调递增
所以函数在(0,2)内单调递减;在[2,+∞)内单调递增.
分析:设0<x1<x2,化简 y1-y2 的解析式到因式乘积的形式,假如0<x1<x2<2,
判断y1-y2的符号,得出结论; 假如2<x1<x2,判断y1-y2 的符号,得出结论.
点评:本题考查利用函数的单调性的定义证明函数的单调性,体现分类讨论的数学思想.

练习册系列答案
相关题目