Question

【题目】已知在平面坐标系内，O为坐标原点，向量 =（1，7）， =（5，1）， =（2，1），点M为直线OP上的一个动点．
（1）当 取最小值时，求向量 的坐标；
（2）在点M满足（I）的条件下，求∠AMB的余弦值．

Answer 1

【答案】
（1）解：设 ，

∵点M为直线OP上的一个动点，

∴向量 与 共线，

∴x﹣2y=0；

即 ，

∴ = ﹣ =（1﹣2y，7﹣y），

=（5﹣2y，1﹣y），

∴ ；

∴当且仅当y=2时得 ，此时 ；

（2）解：当 时， ；

∴ = =﹣ ；

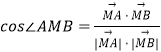∴∠AMB的余弦值为- ．

【解析】（1）设出 ，利用平面向量的坐标表示与运算法则，即可求出对应 的值；（2）利用平面向量的夹角余弦公式，即可求出对应的余弦值．
【考点精析】掌握平面向量的坐标运算是解答本题的根本，需要知道坐标运算：设，则;;设，则．