题目内容
已知函数
(1)若 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若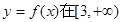 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;
(3)当 有实根,求实数b的最大值。
有实根,求实数b的最大值。
【解析】本试题主要是考查了导数在研究函数中的运用。主要是极值的概念和根据单调区间,求解参数的取值范围,以及利用函数与方程的思想求解参数b的最值。
【答案】
解:(1) ……1分
……1分
因为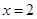 为
为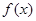 的极值点,所以
的极值点,所以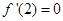
即 ,解得
,解得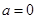 ,又当
,又当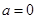 时,
时,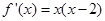 ,从而
,从而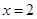 为
为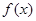 的极值点成立。…………2分
的极值点成立。…………2分
(2)因为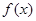 在区间
在区间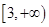 上为增函数,所以
上为增函数,所以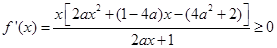 在区间
在区间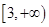 上恒成立。…………3分
上恒成立。…………3分
①当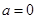 时,
时, 在区间
在区间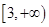 上恒成立,
上恒成立,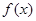 在区间
在区间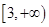 上为增函数,符合题意。…………4分
上为增函数,符合题意。…………4分
②当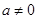 时,由函数
时,由函数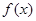 的定义域可知,必有
的定义域可知,必有 对
对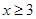 成立,
成立,
故只能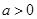 …………5分
…………5分
故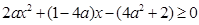 对
对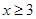 恒成立
恒成立
令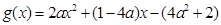 ,其对称轴为
,其对称轴为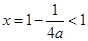
从而要使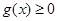 对
对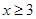 恒成立,只要
恒成立,只要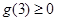 即可…………6分
即可…………6分
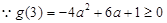 解得:
解得: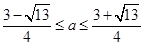
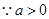 ,故
,故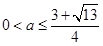
综上所述,实数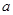 的取值范围为
的取值范围为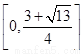 …………7分
…………7分
(3)若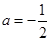 时,方程
时,方程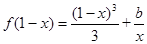 可化为,
可化为,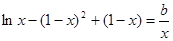 .
.
问题转化为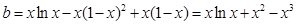 在
在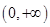 上有解,
上有解,
即求函数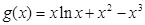 的值域.………………………………8分
的值域.………………………………8分
以下给出两种求函数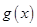 值域的方法:
值域的方法:
解法一: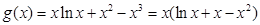 ,令
,令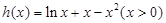
则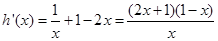 …………9分
…………9分
所以当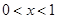 时,
时,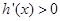 ,从而
,从而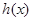 在
在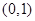 上为增函数
上为增函数
当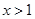 时,
时,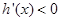 ,从而
,从而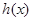 上为减函数
上为减函数
因此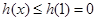 …………10分
…………10分
而 ,故
,故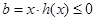 …………11分
…………11分
因此当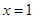 时,
时,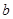 取得最大值
取得最大值 ………12分
………12分
解法二:因为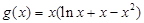 ,所以
,所以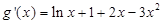
设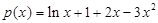 ,则
,则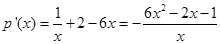 ………9分
………9分
当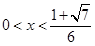 时,
时,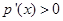 ,所以
,所以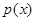 在
在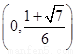 上单调递增
上单调递增
当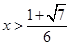 时,
时,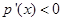 ,所以
,所以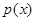 在
在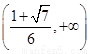 上单调递减
上单调递减
因为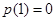 ,故必有
,故必有 ,又
,又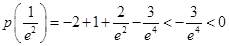 …10分
…10分
因此必存在实数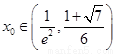 使得
使得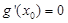
当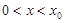 时,
时,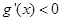 ,所以
,所以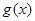 在
在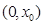 上单调递减;
上单调递减;
当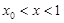 时,
时,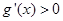 ,所以
,所以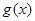 在
在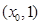 上单调递增
上单调递增
当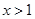 时,
时,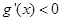 ,所以
,所以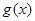 在
在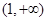 上单调递减………11分
上单调递减………11分
又因为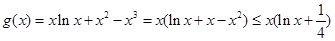
当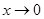 时,
时,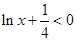 ,则
,则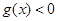 ,又
,又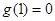
因此当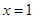 时,
时,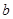 取得最大值
取得最大值

练习册系列答案
相关题目

 的表达式;
的表达式; 上是单调函数.
上是单调函数.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数
 ,求
,求 的零点;
的零点; 上有两个不同的零点,求
上有两个不同的零点,求 的取值范围。
的取值范围。