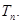题目内容
设数列{ n}满足
n}满足 1=
1= ,
, n+1=
n+1= n2+
n2+ 1,
1,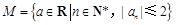 .
.
(Ⅰ)当 ∈(-∞,-2)时,求证:
∈(-∞,-2)时,求证: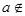 M;
M;
(Ⅱ)当 ∈(0,
∈(0,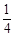 ]时,求证:
]时,求证: ∈M;
∈M;
(Ⅲ)当 ∈(
∈(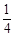 ,+∞)时,判断元素
,+∞)时,判断元素 与集合M的关系,并证明你的结论.
与集合M的关系,并证明你的结论.
 n}满足
n}满足 1=
1= ,
, n+1=
n+1= n2+
n2+ 1,
1,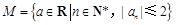 .
.(Ⅰ)当
 ∈(-∞,-2)时,求证:
∈(-∞,-2)时,求证: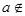 M;
M;(Ⅱ)当
 ∈(0,
∈(0,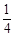 ]时,求证:
]时,求证: ∈M;
∈M;(Ⅲ)当
 ∈(
∈(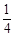 ,+∞)时,判断元素
,+∞)时,判断元素 与集合M的关系,并证明你的结论.
与集合M的关系,并证明你的结论.见解析
(I)如果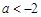 ,则
,则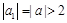 ,
,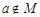 .(2)易采用数学归纳法证明.
.(2)易采用数学归纳法证明.
(3)本小题难度偏大,一般学生解决不了,可以放弃,放弃也是一种勇气,也是一种能力.
本小题的思路是对于任意 ,
,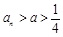 ,且
,且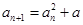 .
.
对于任意 ,
,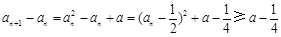 ,
,
则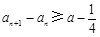 .所以,
.所以,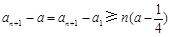 .进行到此,问题基本得以解决
.进行到此,问题基本得以解决
证明:(1)如果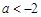 ,则
,则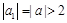 ,
,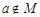 . ……………2分
. ……………2分
(2) 当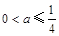 时,
时,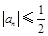 (
(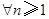 ).
).
事实上,当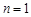 时,
时,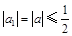 . 设
. 设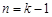 时成立(
时成立(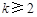 为某整数),
为某整数),
则对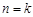 ,
,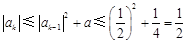 .
.
由归纳假设,对任意n∈N*,|an|≤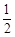 <2,所以a∈M.…………………6分
<2,所以a∈M.…………………6分
(3) 当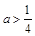 时,
时,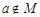 .证明如下:
.证明如下:
对于任意 ,
,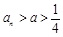 ,且
,且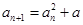 .
.
对于任意 ,
,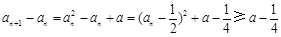 ,
,
则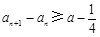 .所以,
.所以,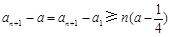 .
.
当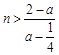 时,
时,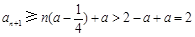 ,即
,即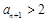 ,因此
,因此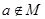
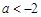 ,则
,则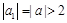 ,
,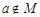 .(2)易采用数学归纳法证明.
.(2)易采用数学归纳法证明.(3)本小题难度偏大,一般学生解决不了,可以放弃,放弃也是一种勇气,也是一种能力.
本小题的思路是对于任意
 ,
,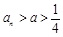 ,且
,且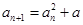 .
.对于任意
 ,
,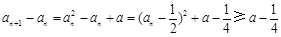 ,
, 则
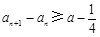 .所以,
.所以,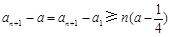 .进行到此,问题基本得以解决
.进行到此,问题基本得以解决证明:(1)如果
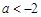 ,则
,则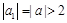 ,
,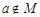 . ……………2分
. ……………2分(2) 当
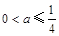 时,
时,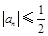 (
(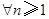 ).
).事实上,当
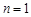 时,
时,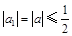 . 设
. 设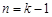 时成立(
时成立(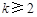 为某整数),
为某整数),则对
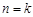 ,
,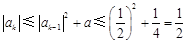 .
.由归纳假设,对任意n∈N*,|an|≤
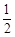 <2,所以a∈M.…………………6分
<2,所以a∈M.…………………6分(3) 当
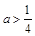 时,
时,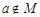 .证明如下:
.证明如下:对于任意
 ,
,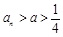 ,且
,且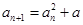 .
.对于任意
 ,
,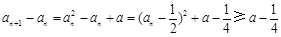 ,
, 则
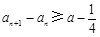 .所以,
.所以,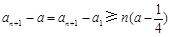 .
.当
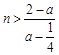 时,
时,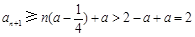 ,即
,即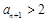 ,因此
,因此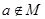

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
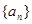 是等差数列,
是等差数列,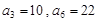 ,数列
,数列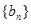 的前n项和是
的前n项和是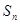 ,且
,且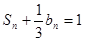 .
.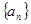 中,
中,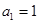 ,且对于任意正整数n,都有
,且对于任意正整数n,都有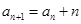 ,则
,则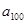 =______
=______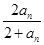 (n∈N*).
(n∈N*).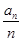 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。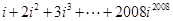 .
. 满足
满足
 ,则数列
,则数列 的最小值是
的最小值是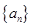 中,其前n项和为
中,其前n项和为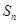 ,若对任意的正整数
,若对任意的正整数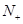 ,均有
,均有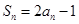 ,则
,则 ;
; 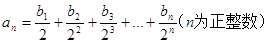 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.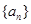 为等比数列,
为等比数列,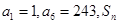 为等差数列
为等差数列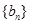 的前n项和,
的前n项和,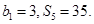
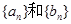 的通项公式;
的通项公式;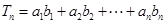 ,求
,求