题目内容
在数列{an}中,a1=1,an+1= 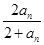 (n∈N*).
(n∈N*).
(Ⅰ)求a2, a3, a4;
(Ⅱ)猜想an,并用数学归纳法证明;
(Ⅲ)若数列bn=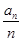 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。
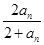 (n∈N*).
(n∈N*).(Ⅰ)求a2, a3, a4;
(Ⅱ)猜想an,并用数学归纳法证明;
(Ⅲ)若数列bn=
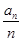 ,求数列{bn}的前n项和sn。
,求数列{bn}的前n项和sn。(Ⅰ)∴a2=  =
=  ,a3 =
,a3 =  =
=  ,a4 =
,a4 = =
= .(Ⅱ)略
.(Ⅱ)略
(Ⅲ)sn=b1+b2+…+bn=2[(1- )+(
)+( -
- )+…+(
)+…+( -
- )]=2[1-
)]=2[1- ]=
]=
 =
=  ,a3 =
,a3 =  =
=  ,a4 =
,a4 = =
= .(Ⅱ)略
.(Ⅱ)略(Ⅲ)sn=b1+b2+…+bn=2[(1-
 )+(
)+( -
- )+…+(
)+…+( -
- )]=2[1-
)]=2[1- ]=
]=
本试题主要是考查了运用递推关系求解数列的前几项,然后根据前几项的特点分析得到数列的通项公式,进而利用数列的归纳猜想思想,和数学归纳法的得到证明,并对于新数列求解和的问题。
(1)首先由a1=1,an+1=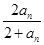 ,,对n赋值依次得到第二项和第三项以及第四项。
,,对n赋值依次得到第二项和第三项以及第四项。
(2)归纳猜想其通项公式,并运用数学归纳法加以证明,
(3)由(Ⅱ)知:bn=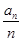 =
= =2[
=2[ -
- ],然后裂项求和得到结论。
],然后裂项求和得到结论。
(1)首先由a1=1,an+1=
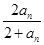 ,,对n赋值依次得到第二项和第三项以及第四项。
,,对n赋值依次得到第二项和第三项以及第四项。(2)归纳猜想其通项公式,并运用数学归纳法加以证明,
(3)由(Ⅱ)知:bn=
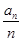 =
= =2[
=2[ -
- ],然后裂项求和得到结论。
],然后裂项求和得到结论。
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 n}满足
n}满足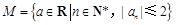 .
.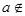 M;
M;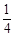 ]时,求证:
]时,求证: 满足:
满足: ,
, 。
。 ;
;  ,求数列
,求数列 的通项公式;
的通项公式;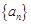 中,
中,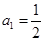 ,
,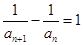 .
. 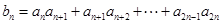 ,求
,求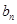 的最大值。
的最大值。 满足
满足 ,则
,则 =
= 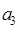 成等差数列.
成等差数列. 的前
的前 项和
项和 ,那么它的通项公式
,那么它的通项公式
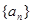 为等差数列且
为等差数列且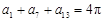 ,则
,则 的值为
的值为

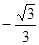
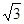
 满足
满足 ,则该数列的前2011项的乘积
,则该数列的前2011项的乘积 = 。
= 。