题目内容
已知函数
（x≠0，常数a∈R），
（1）当a=2时，解不等式f（x）- f（x-1）＞2x-1；
（2）讨论函数f（x）的奇偶性，并说明理由。
（x≠0，常数a∈R），（1）当a=2时，解不等式f（x）- f（x-1）＞2x-1；
（2）讨论函数f（x）的奇偶性，并说明理由。
解：（1）
，
x（x-1）＜0，
∴原不等式的解为0＜x＜1；
（2）当a=0时，
，
对任意
，
，
∴f（x）为偶函数；
当a≠0时，
，
取x=±1，得
，
∴
，
∴函数f（x）既不是奇函数，也不是偶函数。
，x（x-1）＜0，
∴原不等式的解为0＜x＜1；
（2）当a=0时，
，对任意
，，∴f（x）为偶函数；
当a≠0时，
， 取x=±1，得
， ∴
， ∴函数f（x）既不是奇函数，也不是偶函数。
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
恒成立；③若
，
，
，则有
．
与
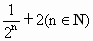的大小；
时，有f(x)＜2x＋2，由此他提出猜想：对一切
，都有f(x)＜2x＋2，请你判断此猜想是否正确，并说明理由．
，则
；