题目内容
请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分.
A.
选修4-1:几何证明选讲
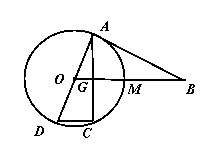 如图,已知
如图,已知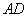 是圆
是圆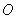 的直径,直线
的直径,直线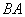 与圆
与圆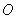 相切于点
相切于点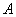 ,直线
,直线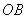 与弦
与弦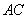 垂直并相交于点
垂直并相交于点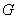 ,与弧
,与弧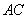 相交于
相交于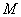 ,连接
,连接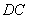 ,
,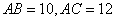 .
.
(Ⅰ)求证: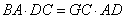 ;
;
(Ⅱ)求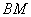 的长.
的长.
B.
选修4-4:坐标系与参数方程
已知曲线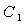 的极坐标方程为
的极坐标方程为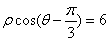 ,曲线
,曲线 的参数方程为
的参数方程为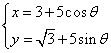 (
(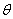 为参数),求
为参数),求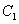 与
与 相交所得弦的弦长.
相交所得弦的弦长.
C.
选修4-5:不等式选讲
已知函数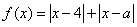 .
.
(Ⅰ)若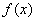 的最小值为
的最小值为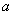 ,求
,求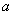 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,求不等式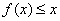 的解集.
的解集.
【答案】
A.解:(Ⅰ)证明:∵直线 与圆
与圆 相切于点
相切于点
∴
又∵ ,
, 是圆
是圆 的直径
的直径
∴ ∴
∴ ∽
∽
∴ 即
即
又∵ ∴
∴ .
——5分
.
——5分
(Ⅱ)在 中,
中, ,
, ,∴
,∴
由 ∽
∽ ,得
,得 ,即
,即
∵
∴ ∴
∴ .
——10分
.
——10分
B.解:曲线 的直角坐标方程为
的直角坐标方程为 ——3分
——3分
曲线 的直角坐标方程为
的直角坐标方程为 ——6分
——6分
曲线 的圆心到直线
的圆心到直线 的距离
的距离
∴弦长等于 .
——10分
.
——10分
C.解:(Ⅰ)
解,得 ——4分
——4分
(Ⅱ)由 或
或 或
或 ∴解集为
∴解集为 ——10分
——10分

练习册系列答案
相关题目
 本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分.
本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分.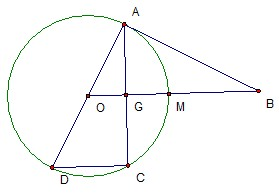 (选做题)请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.
(选做题)请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号. (2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
(2013•长春一模)请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
 (t为参数)被曲线
(t为参数)被曲线 所截的弦长.
所截的弦长. 的最大值;
的最大值;