题目内容
直线 与圆O:x2+y2=4交于A、B两点,则
与圆O:x2+y2=4交于A、B两点,则 =
=
- A.2
- B.-2
- C.4
- D.-4
A
分析:先求圆心到直线的距离,再求弦心距所在直线与AO的夹角,然后求数量积.
解答:圆O:x2+y2=4的圆心是(0,0),由此知圆心到直线 的距离是
的距离是 =
= <2
<2
所以直线与圆相交
故AB=2 =2=r,所以∠AOB=
=2=r,所以∠AOB=
所以 =2×2×cos
=2×2×cos =2
=2
故选A
点评:本题考查直线与圆的位置关系,向量的数量积,基础题.考查了数形结合解题的思想及转化的思想
分析:先求圆心到直线的距离,再求弦心距所在直线与AO的夹角,然后求数量积.
解答:圆O:x2+y2=4的圆心是(0,0),由此知圆心到直线
 的距离是
的距离是 =
= <2
<2所以直线与圆相交
故AB=2
 =2=r,所以∠AOB=
=2=r,所以∠AOB=
所以
 =2×2×cos
=2×2×cos =2
=2故选A
点评:本题考查直线与圆的位置关系,向量的数量积,基础题.考查了数形结合解题的思想及转化的思想

练习册系列答案
相关题目
 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3,
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3,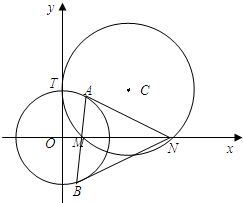 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3,
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M、N(点M在点N的左侧),且|MN|=3,
