题目内容
设函数f（x）=sinx+cosx，若0≤x≤2012π，则函数f（x）的各极值之和为（ ）
分析：先求出其导函数，利用导函数得到其单调区间以及其极值点，进而求出其极值；再利用等比数列的求和公式求出函数f（x）的各极值之和即可．
解答：解：∵函数f（x）=sinx-cosx，
∴f′（x）=（sinx-cosx）′=cosx-sinx，
∵x∈（2kπ+
，2kπ+
）时，f′（x）＜0，x∈（2kπ-
，2kπ+
）时，f′（x）＞0，
∴x∈（2kπ-
，2kπ+
）时原函数递增，x∈（2kπ+
，2kπ+
）时，原函数递减，
故当x=kπ+
时，f（x）取极值，
其极值为f（kπ+
）=sin（kπ+
）-cos（kπ+
）=0
又0≤x≤2012π，
∴函数f（x）的各极值之和S=0+0+0+…+0=0
故答案为 C．
∴f′（x）=（sinx-cosx）′=cosx-sinx，
∵x∈（2kπ+
| π |
| 4 |
| 5π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
∴x∈（2kπ-
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
故当x=kπ+
| π |
| 4 |
其极值为f（kπ+
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
又0≤x≤2012π，
∴函数f（x）的各极值之和S=0+0+0+…+0=0
故答案为 C．
点评：本题主要考查利用导数研究函数的极值以及等比数列求和公式的应用．在求函数的极值时，须注意极值两侧导函数值符号相反
练习册系列答案
相关题目
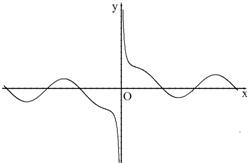如图是函数Q（x）的图象的一部分，设函数f（x）=sinx，g （ x ）=| 1 |
| x |
A、
| ||
| B、f（x）g（x） | ||
| C、f（x）-g（x） | ||
| D、f（x）+g（x） |
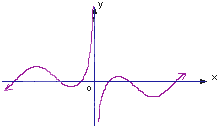设函数f（x）=sinx，g（x）=