题目内容
在△ABC中,A=45°,C=30°,c=20,则边a的长为
- A.
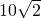
- B.
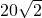
- C.

- D.

B
分析:由A和C的度数求出sinA和sinC的值,然后再由c的长,利用正弦定理即可求出a的长.
解答:由A=45°,C=30°,c=20,
根据正弦定理 =
= 得:
得:
a= =
= =20
=20 .
.
故选B
点评:此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理,牢记特殊角的三角函数值是解本题的关键.
分析:由A和C的度数求出sinA和sinC的值,然后再由c的长,利用正弦定理即可求出a的长.
解答:由A=45°,C=30°,c=20,
根据正弦定理
 =
= 得:
得:a=
 =
= =20
=20 .
.故选B
点评:此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理,牢记特殊角的三角函数值是解本题的关键.

练习册系列答案
相关题目