题目内容
关于平面向量a,b,c,有下列三个命题:
①若a·b=a·c,则b=c;
②若a=(1,k),b=(-2,6),a∥b,则k=-3;
③非零向量a和b满足|a|=|b|=|a-b|,则a与a+b的夹角为30o.
(参若a-(1,k),b=(-2,6),a
其中真命题的序号为( )
| A.①② | B.①③ | C.②③ | D.①②③ |
C
解析试题分析:①当 时,
时, 不一定相等,故①不正确;②若a∥b,则有
不一定相等,故①不正确;②若a∥b,则有 ,解得
,解得 ,故②正确;③令
,故②正确;③令 ,则
,则 ,因为|a|=|b|=|a-b|,所以
,因为|a|=|b|=|a-b|,所以 为正三角形。设以
为正三角形。设以 为临边的平行四边形为
为临边的平行四边形为 ,因为
,因为 为正三角形,所以
为正三角形,所以 为菱形且
为菱形且 。由向量加法的平行四边形法则可知
。由向量加法的平行四边形法则可知 。所以
。所以 。故③正确。
。故③正确。
考点:平面向量的加减法、平行及数量积的计算。

练习册系列答案
相关题目
已知 的面积为2,在
的面积为2,在 所在的平面内有两点
所在的平面内有两点 、
、 ,满足
,满足 ,
, ,则
,则 的面积为( )
的面积为( )
A. | B. | C. | D. |
已知 三个内角A,B,C所对的边,若
三个内角A,B,C所对的边,若 且
且 的面积
的面积 ,则三角形
,则三角形 的形状是( )
的形状是( )
| A.等腰三角形 | B.等边三角形 |
| C.等腰直角三角形 | D.有一个为 的等腰三角形 的等腰三角形 |
在平面直角坐标系xOy中,点A(5,0),对于某个正实数k,存在函数f(x)=a (a>0).使得
(a>0).使得 =λ·(
=λ·( +
+ )(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
)(λ为常数),这里点P、Q的坐标分别为P(1,f(1)),Q(k,f(k)),则k的取值范围为( )
| A.(2,+∞) | B.(3,+∞) | C.[4,+∞) | D.[8,+∞) |
如图所示的方格纸中有定点O,P,Q,E,F,G,H,则 =( )
=( )
A. | B. | C. | D. |
化简 ( )
( )
A. | B. | C. | D. |
若a,b,c均为单位向量,且a·b=0,则|a+b-c|的最小值为( ).
A. -1 -1 | B.1 | C. +1 +1 | D. |
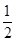 ,则|a+2b|等于( )
,则|a+2b|等于( )