Question

【题目】已知函数f（x）＝4cosxsin（x）+a的最大值为2.

（1）求实数a的值；

（2）在给定的直角坐标系上作出函数f（x）在[0，π]上的图象：

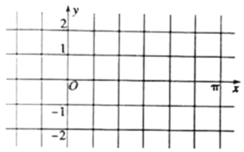
（3）求函数f（x）在[，]上的零点，

Answer 1

【答案】（1）；（2）作图见解析；（3）零点为和.

【解析】

（1）利用正弦的和角公式，以及辅助角公式化简为标准型正弦函数，根据其最大值，即可求得参数；

（2）根据（1）中所求，列表、描点，即可求得函数在区间上的图象；

（3）求出在上的零点，再与取交集即可求得结果.

（1）f（x）＝4cosxsin（x）+a＝4cosx（sinxcosx）+a

＝2sinxcosx+2cos2x+a

sin2x+cos2x+a+1＝2sin（2x）+a+1

则f（x）的最大值为2+a+1＝2，得a＝﹣1.

（2）由（1）可得

列表如下：

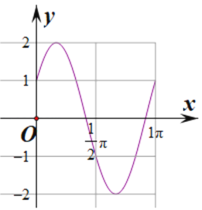
用“五点法”画出函数f（x）在区间[0，π]的简图，如图所示；

（3）由得2xkπ，k∈Z，

则x，k∈Z，

由，得，即k＝0或k＝1，

当k＝0时，x，当k＝1时，x，

即函数在[,]上的零点为和.