题目内容
已知函数f(x)＝ax＋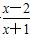
(a>1)．
(1)求证：函数f(x)在(－1，＋∞)上为增函数；
(2)求证：方程f(x)＝0没有负根．
[证明] (1)解法1：任取x1，x2∈(－1，＋∞)，不妨设x1<x2，则x2－x1>0，ax2－x1>1且ax1>0，
∴ax2－ax1＝ax1(ax2－x1－1)>0.
又∵x1＋1>0，x2＋1>0，
求导数得f′(x)＝axlna＋
，
∵a>1，∴当x>－1时，axlna>0，>0，
∴f′(x)>0在(－1，＋∞)上恒成立，
f(x)在(－1，＋∞)上为增函数．
(2)解法1：设存在x0<0(x0≠－1)满足f(x0)＝0，
则ax0＝－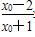
，且0<ax0<1，
∴0<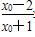－<1，即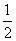
<x0<2，
与假设x0<0矛盾，故方程f(x)＝0没有负根．
解法2：设存在x0<0(x0≠－1)满足f(x0)＝0，
①若－1<x0<0，则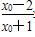<－2，ax0<1，
∴f(x0)<－1与f(x0)＝0矛盾．
②若x0<－1，则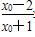>1，ax0>0，
∴f(x0)>1与f(x0)＝0矛盾．
故方程f(x)＝0没有负根.
练习册系列答案
阅读快车系列答案
相关题目
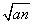，an＋1)(n∈N＋)在函数y＝x2＋1的图像上．
.
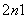