题目内容
12．若0＜x，y，z＜1，求证：x（1-y），y（1-z），z（1-x）不可能都大于$\frac{1}{4}$．分析 利用反证法，先对结论进行否定，再利用基本不等式，推出矛盾即可．
解答 证明：假设三个式子都大于$\frac{1}{4}$，
即（1-x）y＞$\frac{1}{4}$，（1-y）z＞$\frac{1}{4}$，（1-z）x＞$\frac{1}{4}$，
三个式子相乘得：
（1-x）y•（1-y）z•（1-z）x＞$\frac{1}{{4}^{3}}$ ①
∵0＜x＜1，∴x（1-x）≤（$\frac{x+1-x}{2}$）2=$\frac{1}{4}$
同理：y（1-y）≤$\frac{1}{4}$，z（1-z）≤$\frac{1}{4}$，
∴（1-x）y•（1-y）z•（1-z）x≤$\frac{1}{{4}^{3}}$ ②
显然①与②矛盾，所以假设是错误的，故原命题成立．
点评 本题考查用反证法证明数学命题，把要证的结论进行否定，在此基础上推出矛盾，是解题的关键．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
如图所示，四棱锥S-ABCD中，底面ABCD为正方形，且AB=4，SA⊥平面ABCD，∠SDA=60°，E、F、G分别是SC、SD、AC上的点，且$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$．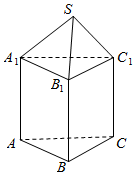
如图所示的几何体是由一个正三棱锥S-A1B1C1和一个所有棱长都相等的正三棱柱ABC-A1B1C1组合而成，且该几何体的外接球（几何体的所有顶点都在该球面上）的表面积为7π，则三棱锥S-A1B1C1的体积为$\frac{\sqrt{21}-3}{8}$．