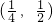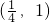题目内容
已知不等式logx（4x）＜0成立，则实数x的取值范围是（ ）A．
B．
C．
D．
【答案】分析：当x＞1时，求出不等式的解集；当1＞x＞0时，再求出不等式的解集，把这两个解集取并集即得所求．
解答：解：当x＞1时，4x＞4，logx（4x）＜0 不可能，解集为∅．
当1＞x＞0时，∵logx（4x）＜0，∴1＜4x，∴
＜x，故解集为
．
综上，不等式的解集为
=
，
故选：D．
点评：本题主要考查对数函数的单调性和特殊点，体现了分类讨论的数学思想，分类讨论是解题的关键．
解答：解：当x＞1时，4x＞4，logx（4x）＜0 不可能，解集为∅．
当1＞x＞0时，∵logx（4x）＜0，∴1＜4x，∴
＜x，故解集为．综上，不等式的解集为
=，故选：D．
点评：本题主要考查对数函数的单调性和特殊点，体现了分类讨论的数学思想，分类讨论是解题的关键．
练习册系列答案
相关题目
