题目内容

解析:(Ⅰ)当![]() 时,由
时,由![]() ,解得
,解得![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() .
.
两式相减,并利用![]() ,求得
,求得![]() .
.
∴数列![]() 是首项为2,公差为1的等差数列.∴
是首项为2,公差为1的等差数列.∴![]() (
(![]() ).
).
(Ⅱ)∵![]() 是首项为2,公比为2的等比数列,∴
是首项为2,公比为2的等比数列,∴![]() .
.
当n为偶数时,![]()
![]()
![]() .
.
(Ⅲ)∵![]() (n为偶数),
(n为偶数),
设![]() (n为偶数),
(n为偶数),
∴![]() .且
.且![]() ,
,
(利用数列的单调性或函数的单调性判断)
∴![]() ,即
,即![]() (n为偶数).
(n为偶数).
因此同学乙的观点正确

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
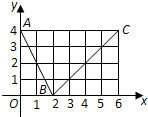 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=