题目内容
(本小题满分12分)袋子中装有大小相同的白球和红球共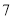 个,从袋子中任取
个,从袋子中任取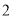 个球都是白球的概率为
个球都是白球的概率为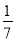 ,每个球被取到的机会均等.现从袋子中每次取
,每个球被取到的机会均等.现从袋子中每次取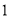 个球,如果取出的是白球则不再放回,设在取得红球之前已取出的白球个数为
个球,如果取出的是白球则不再放回,设在取得红球之前已取出的白球个数为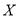 .
.
(1)求袋子中白球的个数;
(2)求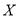 的分布列和数学期望.
的分布列和数学期望.
(1) ;(2)分布列见解析,
;(2)分布列见解析, .
.
【解析】
试题分析:(1)利用从袋子中任取 个球都是白球的概率为
个球都是白球的概率为 ,计算出袋子中白球的个数;(2)先分析确定随机变量的所有可能取值,再计算各个取值的概率,即可得其分布列,利用数学期望公式求数学期望.
,计算出袋子中白球的个数;(2)先分析确定随机变量的所有可能取值,再计算各个取值的概率,即可得其分布列,利用数学期望公式求数学期望.
试题解析:(1)【解析】
设袋子中有
 N
N 个白球,依题意得,
个白球,依题意得, , 1分
, 1分
即 , 化简得,
, 化简得, , 2分
, 2分
解得, 或
或 (舍去). 3分
(舍去). 3分
∴袋子中有 个白球. 4分
个白球. 4分
(2)【解析】
由(1)得,袋子中有 个红球,
个红球, 个白球. 5分
个白球. 5分
 的可能取值为
的可能取值为 , 6分
, 6分
 ,
,  ,
,
 ,
, . 10分
. 10分
∴ 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
∴ . 12分
. 12分
考点:1、古典概型;2、解方程;3、离散型随机变量的分布列与数学期望.
考点分析: 考点1:古典概率 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目










 ,
, .
. ;
; 在
在 恒成立,求
恒成立,求 的最小值.
的最小值. ,
, ,若
,若 ,则
,则 为( )
为( ) B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,
, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 Z
Z 为偶函数,且在区间
为偶函数,且在区间 上是单调增函数,则
上是单调增函数,则 的值为 .
的值为 . 上存在点
上存在点 满足约束条件
满足约束条件 则实数
则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 的外接圆半径为1,圆心为
的外接圆半径为1,圆心为 ,且
,且 ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 与曲线
与曲线 有四个不同交点,则实数
有四个不同交点,则实数 的取值范围是 ( ).
的取值范围是 ( ). B.
B. C.
C. D.
D.