Question

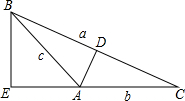写出正弦定理，并对钝角三角形的情况加以证明．

Answer 1

分析：先写出正弦定理，然后证明．先分别作BC、AC边上的高线，根据三角形的面积公式分别表示出以BC、AC、AB为底边的面积，然后根据同一个三角形的面积相等得到等式

1

2

bcsinA=

1

2

acsinB=

1

2

absinC，最后同时除以

1

2

abc可得证．

解答：解：

sinA

a

=

sinB

b

=

sinC

c

．
证：引AD垂直BC于D；引BE垂直CA的延长线于E．
设△ABC的面积为S，则S=

1

2

AC•BE=

1

2

bcsin(180°-A)=

1

2

bcsinA；
又S=

1

2

BC•AD=

1

2

acsinBS=

1

2

BC•AD=

1

2

absinC
∴S=

1

2

bcsinA=

1

2

acsinB=

1

2

absinC，
将上式除以

1

2

abc，得：

sinA

a

=

sinB

b

=

sinC

c

．

点评：本题主要考查正弦定理的证明．属基础题．