题目内容
(本题满分18分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分7分
已知曲线 的方程为
的方程为 ,
, 、
、 为曲线上的两点,
为曲线上的两点, 为坐标原点,且有
为坐标原点,且有 .
.
(1)若 所在直线的方程为
所在直线的方程为 ,求
,求 的值;
的值;
(2)若点 为曲线
为曲线 上任意一点,求证:
上任意一点,求证: 为定值;
为定值;
(3)在(2)的基础上,用类比或推广的方法对新的圆锥曲线 写出一个命题,并对该命题加以证明.
写出一个命题,并对该命题加以证明.
解:(1)∵ 所在直线的方程为
所在直线的方程为
由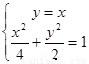 可得
可得 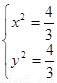 ∴
∴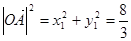 …………2分
…………2分
又 ∵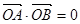 ∴
∴ ∴
∴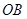 所在直线的方程为
所在直线的方程为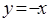 ,
,
同理可得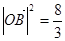 ……………4分
……………4分
∴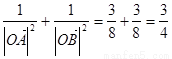 ……………5分
……………5分
(2)当点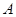 在
在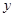 轴上时,点
轴上时,点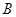 在
在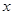 轴上,此时有
轴上,此时有 ,
,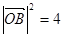 ,
,
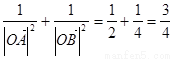 ……………6分
……………6分
当点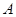 不在
不在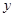 轴上时,设
轴上时,设 所在直线的方程为
所在直线的方程为 ,则
,则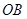 所在直线的方程为
所在直线的方程为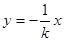 ,
,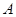 、
、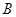 两点的坐标分别为
两点的坐标分别为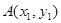 、
、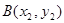
由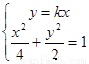 可得
可得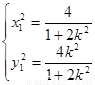 , ∴
, ∴ 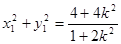 ……………8分
……………8分
同理,由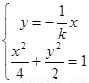 可得
可得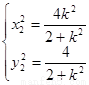 , ∴
, ∴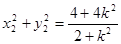 ……………9分
……………9分
∴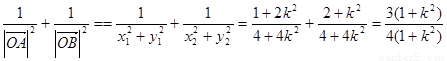
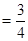 为定值………11分
为定值………11分
(3)根据所写新命题的思维层次的不同情况分别进行评分
①已知双曲线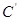 的方程为
的方程为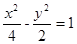 ,
,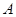 、
、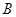 为曲线上的两点,
为曲线上的两点,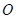 为坐标原点,且有
为坐标原点,且有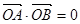 。求证:
。求证: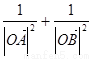 为定值。
……………13分
为定值。
……………13分
证明:显然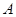 、
、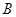 两点都不能在
两点都不能在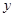 轴上,
轴上,
设 所在直线的方程为
所在直线的方程为 ,则
,则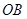 所在直线的方程为
所在直线的方程为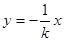 ,
,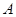 、
、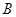 两点的坐标分别为
两点的坐标分别为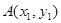 、
、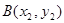
由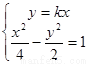 可得
可得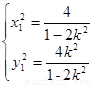 ,
, 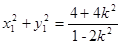 ……………14分
……………14分
同理,由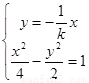 可得
可得 ,
, 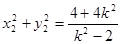
∴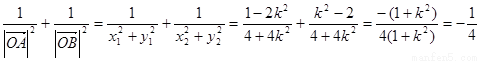 ………15分
………15分
②已知椭圆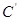 的方程为
的方程为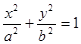 ,
,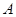 、
、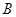 为曲线上的两点,
为曲线上的两点,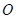 为坐标原点,且有
为坐标原点,且有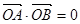 。
。
求证: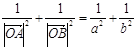 ……………13分
……………13分
证明:当点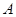 在
在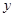 轴上时,点
轴上时,点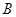 在
在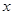 轴上,
轴上,
此时有 ,
,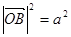 ,
, 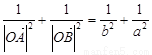 ……………14分
……………14分
当点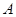 不在
不在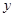 轴上时,设
轴上时,设 所在直线的方程为
所在直线的方程为 ,
,
则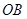 所在直线的方程为
所在直线的方程为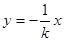 ,
,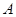 、
、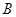 两点的坐标分别为
两点的坐标分别为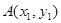 、
、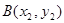
由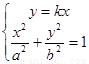 可得
可得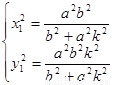 ,
,
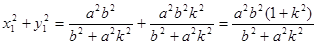 ……………15分
……………15分
同理,由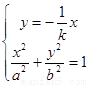 可得
可得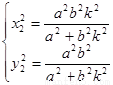
 , ……………16分
, ……………16分
∴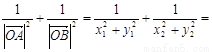
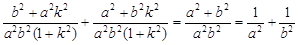 …17分
…17分
③已知双曲线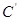 的方程为
的方程为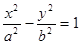 ,
,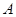 、
、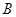 为曲线上的两点,
为曲线上的两点,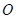 为坐标原点,且有
为坐标原点,且有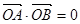 ,
,
则当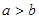 时,求证:
时,求证: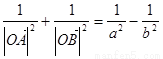 ……………14分
……………14分
证明:显然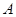 、
、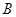 两点都不能在
两点都不能在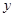 轴上,
轴上,
设 所在直线的方程为
所在直线的方程为 ,则
,则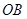 所在直线的方程为
所在直线的方程为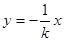 ,
,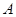 、
、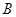 两点的坐标分别为
两点的坐标分别为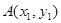 、
、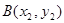
由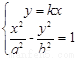 可得
可得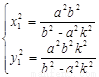 ,
, 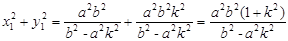 ……15分
……15分
同理,由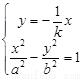 可得
可得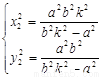
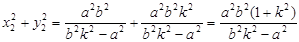 , ……………17分
, ……………17分
故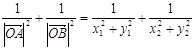
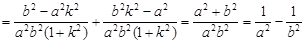 ……………18分
……………18分
【解析】略

 名校课堂系列答案
名校课堂系列答案 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处