Question

（2013•肇庆二模）设过点（0，b）且斜率为1的直线与圆x²+y²-2x=0相切，则b的值为（　　）

• A．2±

  2

• B．2±2

  2

• C．-1±

  2

• D．

  2

  ±1

Answer 1

分析：将圆化成标准方程得（x-1）²+y²=1，得到圆心为C（1，0）且半径r=1．将过点（0，b）且斜率为1的直线化成一般方程得x-y+b=0，结合题意由点到直线的距离公式建立关于b的等式，解之即可得到b=-1±

2

．

解答：解：∵直线过点（0，b）且斜率为1，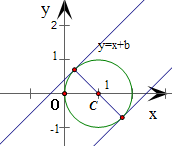
∴设直线为l，得其方程为y=x+b，即x-y+b=0
∵圆x²+y²-2x=0化成标准方程，得（x-1）²+y²=1
∴圆x²+y²-2x=0的圆心为C（1，0），半径r=1
由直线l与圆相切，可得点C到直线l的距离等于半径，
即

|1-0+b|

2

=1，解之得b=-1±

2

故选：C

点评：本题给出斜率为1且过点（0，b）的直线与已知圆相切，求参数b的值，着重考查了直线的方程、圆的方程与直线与圆的位置关系等知识，属于中档题．