题目内容
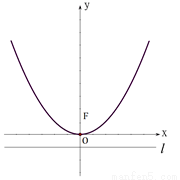
如图,抛物线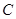 的顶点为坐标原点
的顶点为坐标原点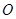 ,焦点
,焦点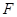 在
在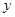 轴上,准线
轴上,准线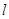 与圆
与圆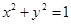 相切.
相切.
(Ⅰ)求抛物线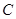 的方程;
的方程;
(Ⅱ)已知直线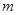 和抛物线
和抛物线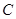 交于点
交于点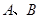 ,命题P:“若直线
,命题P:“若直线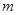 过定点
过定点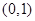 ,则
,则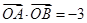 ”,请判断命题P的真假,并证明。
”,请判断命题P的真假,并证明。
【答案】
(Ⅰ) (Ⅱ)命题P为真命题
(Ⅱ)命题P为真命题
【解析】
试题分析:(Ⅰ)依题意,可设抛物线 的方程为
的方程为 ,
,
其准线 的方程为
的方程为 .
.
∵准线 与圆
与圆 相切,
相切,
∴所以圆心 到直线
到直线 的距离
的距离 ,解得
,解得 .
.
故抛物线 的方程为:
的方程为: .
.
(Ⅱ)命题P为真命题
因为直线 和抛物线
和抛物线 交于点
交于点 且过定点
且过定点 ,所以直线
,所以直线 的斜率
的斜率 一定存在
一定存在
设直线 ,交点
,交点 联立抛物线
联立抛物线 的方程
的方程 ,
,
得
 恒成立
恒成立
由韦达定理得

 ,所以命题P为真命题
,所以命题P为真命题
考点:直线与圆锥曲线的综合问题;恒过定点的直线;抛物线的标准方程.
点评:本题考查了抛物线方程的求法,以及直线与抛物线的位置关系判断,做题时要认真分析,避免不必要的错误.

练习册系列答案
相关题目
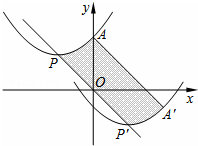 如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为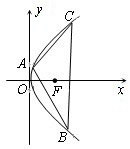
 的顶点为坐标原点
的顶点为坐标原点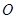 ,焦点
,焦点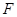 在
在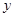 轴上,准线
轴上,准线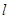 与圆
与圆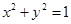 相切.
相切.
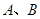 在抛物线
在抛物线 ,求点
,求点 的坐标.
的坐标.