题目内容
已知α为锐角,向量 =(sinα,cosα),
=(sinα,cosα), =(cos2α,sin2α),且
=(cos2α,sin2α),且
(1)求α的值.
(2)若
 ,求向量
,求向量 与
与 的夹角的余弦值.
的夹角的余弦值.
【答案】分析:(1)根据数量积的坐标运算公式,结合向量 、
、 互相垂直,得
互相垂直,得 =sin3α=0,结合α为锐角,得3α=π,可得α=
=sin3α=0,结合α为锐角,得3α=π,可得α= ;
;
(2)由向量模的公式,可得向量 、
、 的模均为1,可得
的模均为1,可得 =(2
=(2 +2
+2 )(2
)(2 +2
+2 )=8
)=8 ,再计算出向量
,再计算出向量 与
与 的模都等于4,结合两个向量的夹角公式即可算出
的模都等于4,结合两个向量的夹角公式即可算出 与
与 的夹角的余弦值.
的夹角的余弦值.
解答:解:(1)∵ ,
, =(sinα,cosα),
=(sinα,cosα), =(cos2α,sin2α),
=(cos2α,sin2α),
∴ =sinαcos2α+cosαsin2α=0,即sin3α=0
=sinαcos2α+cosαsin2α=0,即sin3α=0
∵α为锐角,得3α∈(0, )
)
∴3α=π,可得α=
(2)∵α= ,得
,得 =(sinα,cosα)=(
=(sinα,cosα)=( ,
, ),
), =(cos2α,sin2α)=(-
=(cos2α,sin2α)=(- ,
, ),
),
∴| |=|
|=| |=1,且
|=1,且 =0
=0
因此, =(2
=(2 +2
+2 )(2
)(2 +2
+2 )
)
=4
 +16
+16 +4
+4
 =8
=8
而且| |=
|= =4,|
=4,| |=
|= =4
=4
设向量 与
与 的夹角为θ,可得cosθ=
的夹角为θ,可得cosθ= =
= =
=
即向量 与
与 的夹角的余弦值为
的夹角的余弦值为 .
.
点评:本题给出两个向量含有三角函数的坐标形式,求它们的线性组合向量的夹角余弦之值,着重考查了平面向量数量积的运算、两角和的正弦函数公式和向量夹角公式等知识,属于基础题.
 、
、 互相垂直,得
互相垂直,得 =sin3α=0,结合α为锐角,得3α=π,可得α=
=sin3α=0,结合α为锐角,得3α=π,可得α= ;
;(2)由向量模的公式,可得向量
 、
、 的模均为1,可得
的模均为1,可得 =(2
=(2 +2
+2 )(2
)(2 +2
+2 )=8
)=8 ,再计算出向量
,再计算出向量 与
与 的模都等于4,结合两个向量的夹角公式即可算出
的模都等于4,结合两个向量的夹角公式即可算出 与
与 的夹角的余弦值.
的夹角的余弦值.解答:解:(1)∵
 ,
, =(sinα,cosα),
=(sinα,cosα), =(cos2α,sin2α),
=(cos2α,sin2α),∴
 =sinαcos2α+cosαsin2α=0,即sin3α=0
=sinαcos2α+cosαsin2α=0,即sin3α=0∵α为锐角,得3α∈(0,
 )
)∴3α=π,可得α=

(2)∵α=
 ,得
,得 =(sinα,cosα)=(
=(sinα,cosα)=( ,
, ),
), =(cos2α,sin2α)=(-
=(cos2α,sin2α)=(- ,
, ),
),∴|
 |=|
|=| |=1,且
|=1,且 =0
=0因此,
 =(2
=(2 +2
+2 )(2
)(2 +2
+2 )
)=4

 +16
+16 +4
+4
 =8
=8
而且|
 |=
|= =4,|
=4,| |=
|= =4
=4设向量
 与
与 的夹角为θ,可得cosθ=
的夹角为θ,可得cosθ= =
= =
=
即向量
 与
与 的夹角的余弦值为
的夹角的余弦值为 .
.点评:本题给出两个向量含有三角函数的坐标形式,求它们的线性组合向量的夹角余弦之值,着重考查了平面向量数量积的运算、两角和的正弦函数公式和向量夹角公式等知识,属于基础题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
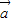 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), =(
=( ,-
,- ).
).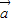 •
• =
= ,
, •
•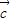 =
=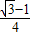 ,求角2β-α的值;
,求角2β-α的值;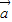 =
= +
+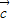 ,求tanα的值.
,求tanα的值.