题目内容
已知α、β为锐角,向量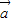 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),
=(cosβ,sinβ), =(
=( ,-
,- ).
).(1)若
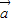 •
• =
= ,
, •
•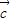 =
=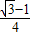 ,求角2β-α的值;
,求角2β-α的值;(2)若
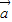 =
= +
+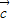 ,求tanα的值.
,求tanα的值.
【答案】分析:(1)由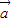 •
•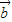 =(cosα,sinα)•(cosβ,sinβ)=cosαcosβ+sinαsinβ=cos(α-β)=
=(cosα,sinα)•(cosβ,sinβ)=cosαcosβ+sinαsinβ=cos(α-β)=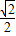 ,可得
,可得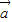 •
•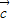 =(cosα,sinα)•(
=(cosα,sinα)•( ,-
,- )=
)= cosα-
cosα- sinα=
sinα=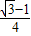 ,α、β为锐角,可得α与β的值,从而即可求角2β-α的值.
,α、β为锐角,可得α与β的值,从而即可求角2β-α的值.
(2)由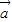 =
=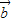 +
+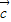 可得
可得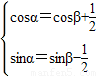 ,③2+④2得cosα-sinα=
,③2+④2得cosα-sinα= ,可得2sinαcosα=
,可得2sinαcosα= .又2sinαcosα=
.又2sinαcosα=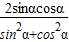
=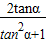 =
= ,可得3tan2α-8tanα+3=0,又α为锐角,即可求出tanα的值.
,可得3tan2α-8tanα+3=0,又α为锐角,即可求出tanα的值.
解答:解:(1)∵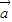 •
•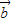 =(cosα,sinα)•(cosβ,sinβ),
=(cosα,sinα)•(cosβ,sinβ),
=cosαcosβ+sinαsinβ
=cos(α-β)=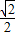 ,①
,①
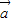 •
•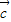 =(cosα,sinα)•(
=(cosα,sinα)•( ,-
,- ),
),
= cosα-
cosα- sinα=
sinα=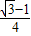 ,②
,②
又∵0<α<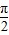 ,0<β<
,0<β<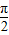 ,
,
∴-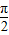 <α-β<
<α-β<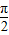 .
.
由①得α-β=±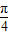 ,由②得α=
,由②得α=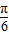 .
.
由α、β为锐角,∴β=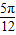 .
.
从而2β-α= π.
π.
(2)由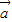 =
=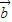 +
+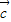 可得
可得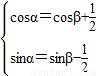 ,
,
③2+④2得cosα-sinα= ,∴2sinαcosα=
,∴2sinαcosα= .
.
又∵2sinαcosα=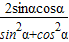
=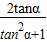 =
= ,
,
∴3tan2α-8tanα+3=0.
因为cosα-sinα>0 所以cosα>sinα又因为α为锐角,所以tanα<1,
又∵α为锐角,∴tanα>0,
∴tanα=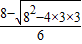
=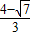 .
.
点评:本题考查了两角函数和与差的运算及平面向量数量积的运算,难度一般,关键是掌握两角和与差的余弦函数公式.
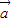 •
•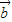 =(cosα,sinα)•(cosβ,sinβ)=cosαcosβ+sinαsinβ=cos(α-β)=
=(cosα,sinα)•(cosβ,sinβ)=cosαcosβ+sinαsinβ=cos(α-β)=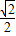 ,可得
,可得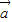 •
•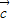 =(cosα,sinα)•(
=(cosα,sinα)•( ,-
,- )=
)= cosα-
cosα- sinα=
sinα=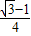 ,α、β为锐角,可得α与β的值,从而即可求角2β-α的值.
,α、β为锐角,可得α与β的值,从而即可求角2β-α的值.(2)由
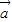 =
=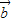 +
+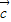 可得
可得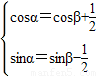 ,③2+④2得cosα-sinα=
,③2+④2得cosα-sinα= ,可得2sinαcosα=
,可得2sinαcosα= .又2sinαcosα=
.又2sinαcosα=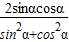
=
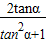 =
= ,可得3tan2α-8tanα+3=0,又α为锐角,即可求出tanα的值.
,可得3tan2α-8tanα+3=0,又α为锐角,即可求出tanα的值.解答:解:(1)∵
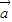 •
•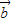 =(cosα,sinα)•(cosβ,sinβ),
=(cosα,sinα)•(cosβ,sinβ),=cosαcosβ+sinαsinβ
=cos(α-β)=
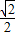 ,①
,①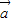 •
•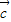 =(cosα,sinα)•(
=(cosα,sinα)•( ,-
,- ),
),=
 cosα-
cosα- sinα=
sinα=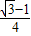 ,②
,②又∵0<α<
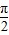 ,0<β<
,0<β<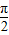 ,
,∴-
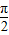 <α-β<
<α-β<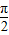 .
.由①得α-β=±
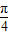 ,由②得α=
,由②得α=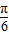 .
.由α、β为锐角,∴β=
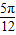 .
.从而2β-α=
 π.
π.(2)由
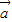 =
=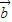 +
+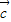 可得
可得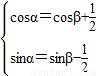 ,
,③2+④2得cosα-sinα=
 ,∴2sinαcosα=
,∴2sinαcosα= .
.又∵2sinαcosα=
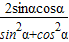
=
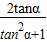 =
= ,
,∴3tan2α-8tanα+3=0.
因为cosα-sinα>0 所以cosα>sinα又因为α为锐角,所以tanα<1,
又∵α为锐角,∴tanα>0,
∴tanα=
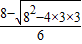
=
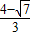 .
.点评:本题考查了两角函数和与差的运算及平面向量数量积的运算,难度一般,关键是掌握两角和与差的余弦函数公式.

练习册系列答案
相关题目
 的单调增区间是
的单调增区间是 .
. 的图象,需把函数
的图象,需把函数 的图象上所有点向左平行移动
的图象上所有点向左平行移动 个单位长度.
个单位长度. ,当
,当 时,函数
时,函数 的最小值为
的最小值为 .
. 、
、 、
、 是锐角
是锐角 的三个内角,则点
的三个内角,则点 在第四象限.
在第四象限.