题目内容
11.在△ABC中,已知三个内角A,B,C所对的边分别为a,b,c,若$A=\frac{π}{3},a=3$,$c=\sqrt{6}$,则角C=( )| A. | $\frac{π}{4}$或$\frac{3π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 利用正弦定理求出sinC的值,即可确定出C的度数.
解答 解:∵$A=\frac{π}{3},a=3$,$c=\sqrt{6}$,
∴a>c,
∴A>C
由正弦定理可得$\frac{a}{sinA}$=$\frac{c}{sinC}$,
∴sinC=$\frac{csinA}{a}$=$\frac{\sqrt{6}×\frac{\sqrt{3}}{2}}{3}$=$\frac{\sqrt{2}}{2}$,
∴C=$\frac{π}{4}$
故选:C
点评 此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
1.某程序框图如图所示,则该程序运行后输出的值是( )


| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
19.设函数f(x)=2lnx-$\frac{3}{x}$-m,若关于x的方程f(f(x))=x恰有两个不相等的实数根,则m的取值范围是( )
| A. | (2ln3-4,+∞) | B. | (-∞,2ln3-4) | C. | (-4,+∞) | D. | (-∞,-4) |
20.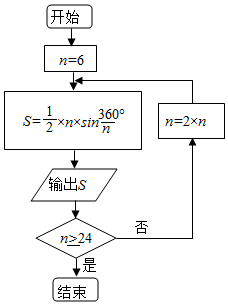 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )| A. | 2.598,3,3.1048 | B. | 2.598,3,3.1056 | C. | 2.578,3,3.1069 | D. | 2.588,3,3.1108 |
1.下列语句不是命题的是( )
| A. | -3>4 | B. | 0.3是整数 | C. | a>3 | D. | 4是3的约数 |