题目内容
19.已知数列{an}满足an=3n-2n+1,求{an}的前n项和Sn.分析 利用等比数列的前n项和公式即可得出.
解答 解:∵an=3n-2n+1,
∴{an}的前n项和Sn=$\frac{3({3}^{n}-1)}{3-1}$-$\frac{4({2}^{n}-1)}{2-1}$
=$\frac{1}{2}({3}^{n+1}-3)$-2n+2+4.
点评 本题考查了等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.设A、B、C是圆O:x2+y2=1上不同的三个点,|$\overrightarrow{OA}$+$\overrightarrow{OB}$|=|$\sqrt{2}$$\overrightarrow{OC}$|,若存在实数λ、μ满足$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,则点P(λ,μ)与圆O的位置关系是( )
| A. | 点P在圆内 | B. | 点P在圆上 | C. | 点P在圆外 | D. | 不确定 |
11.已知l、m、n是空间不同的三条直线,则下列结论中正确的( )
| A. | 若m⊥l,n⊥l,则m⊥n | B. | 若m⊥l,n⊥l,则m∥n | C. | 若m⊥l,n∥l,则m⊥n | D. | 若m⊥l,n∥l,则m∥n |
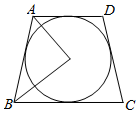 一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)
一个圆内切于一个等腰锑形,已知圆面积是等腰锑形面积的$\frac{1}{2}$,求等腰梯形的底角(用反正切表示)