题目内容
13．已知数列{an}的通项an=2n+1，bn=$\frac{1}{n}$（a1+a2+…+an），则{bn}的前n项和为$\frac{1}{2}$n（n+5）．分析 运用等差数列的求和公式可得bn=n+2，再由等差数列的求和公式，计算即可得到结论．
解答 解：an=2n+1，可得
bn=$\frac{1}{n}$（a1+a2+…+an）=$\frac{1}{n}$•（na1+$\frac{1}{2}$n（n-1）•2）
=a1+n-1=2+n，
则{bn}的前n项和为$\frac{1}{2}$n（3+2+n）=$\frac{1}{2}$n（n+5）．
故答案为：$\frac{1}{2}$n（n+5）．
点评 本题考查等差数列的通项和求和公式的运用，考查运算能力，属于基础题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
3．下列说法不正确的是（ ）
| A． | 如果一条直线上有两个点在一个平面内，则直线在平面内 | |
| B． | 经过两条相交直线有且只有一个平面 | |
| C． | 不共线的三个点可以确定一个平面 | |
| D． | 两个平面可以相交于一个点 |
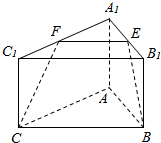如图所示，三棱柱ABC-A1B1C1中，E，F分别是A1B1，A1C1的中点．截面BCFE将三棱柱分成两部分，你能说出多面体A1EF-ABC是什么样的几何体吗？多面体B1C1FE-BC是简单几何体还是组合体？为什么？