题目内容
已知各项均为正数的数列{an}满足：a1＝3，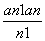
＝
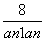(n∈N*)，设bn＝
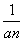，Sn＝b
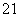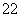＋b
＋…＋b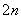
.
(1)求数列{an}的通项公式；
(2)求证：Sn<
.
解析：(1)由题意可得：
①
时, 
②
①─②得
，
，
是首项为
，公比为
的等比数列，
（2）由(1)知
若
为等差数列，
则成等差数列, 
得 
又时，
，显然
成等差数列，
故存在实数，使得数列成等差数列.
练习册系列答案
相关题目
满足的约束条件
当目标函数
在该约束条件下取得最小值
时，
的最小值为( )
D.2 
的前n项和为
,且
,
.
前n项和为
,且 
(
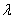为常数).令
.求数列
的前n项和
.
满足
=
（n∈N*）且
，则
为( )
（
是非零常数）与圆
有公共点，且公共点的横坐标和纵坐标均为整数，那么这样的直线共有( )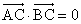
，
，
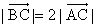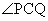的平分线垂直于OA，是否总存在实数
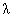，使得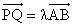
？请说明理由；
,
.若方程
有两个不相等的实根，则实数k的取值范围是
B. 
C.
D. 
的最小正周期是( )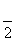
B．π C．2π D．4π