题目内容
若θ是钝角,则满足等式log2(x2-x+2)=sinθ- cosθ的实数x的取值范围是
cosθ的实数x的取值范围是
- A.(-1,2)
- B.(-1,0)∪(1,2)
- C.[0,1]
- D.[-1,0)∪(1,2]
D
分析:利用两角差的正弦函数化简sinθ- cosθ为一个角的一个三角函数的形式,结合θ是钝角,求出表达式的范围,得到x2-x+2的范围,然后求出x的范围即可.
cosθ为一个角的一个三角函数的形式,结合θ是钝角,求出表达式的范围,得到x2-x+2的范围,然后求出x的范围即可.
解答:因为sinθ- cosθ=2sin(θ-
cosθ=2sin(θ- ),θ是钝角,
),θ是钝角,
∴θ- ∈(
∈( ),2sin(θ-
),2sin(θ- )∈(1,2]
)∈(1,2]
log2(x2-x+2)=sinθ- cosθ,可得,
cosθ,可得,
2<x2-x+2≤4,
解2<x2-x+2得x∈(-∞,0)∪(1,+∞).
解x2-x+2≤4,解得x∈[-1,2].
所以所求x的范围是:[-1,0)∪(1,2],
故选D.
点评:本题是中档题,考查三角函数的化简求值,对数函数的范围的求法,考查计算能力.
分析:利用两角差的正弦函数化简sinθ-
 cosθ为一个角的一个三角函数的形式,结合θ是钝角,求出表达式的范围,得到x2-x+2的范围,然后求出x的范围即可.
cosθ为一个角的一个三角函数的形式,结合θ是钝角,求出表达式的范围,得到x2-x+2的范围,然后求出x的范围即可.解答:因为sinθ-
 cosθ=2sin(θ-
cosθ=2sin(θ- ),θ是钝角,
),θ是钝角,∴θ-
 ∈(
∈( ),2sin(θ-
),2sin(θ- )∈(1,2]
)∈(1,2]log2(x2-x+2)=sinθ-
 cosθ,可得,
cosθ,可得,2<x2-x+2≤4,
解2<x2-x+2得x∈(-∞,0)∪(1,+∞).
解x2-x+2≤4,解得x∈[-1,2].
所以所求x的范围是:[-1,0)∪(1,2],
故选D.
点评:本题是中档题,考查三角函数的化简求值,对数函数的范围的求法,考查计算能力.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
若O是△ABC所在平面内的一点,且向量
,
,
满足条件
+
=-
,|
|=|
|=|
|,则△ABC的形状是( )
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| A、钝角三角形 |
| B、锐角三角形 |
| C、直角三角形 |
| D、等边三角形 |
 内有一点
内有一点 ,满足
,满足 ,且
,且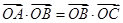 ,则
,则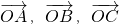 满足条件
满足条件 ,
, ,则△ABC的形状是
,则△ABC的形状是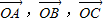 满足条件
满足条件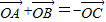 ,
,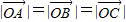 ,则△ABC的形状是( )
,则△ABC的形状是( )