题目内容
【题目】为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了![]() 天空气中的
天空气中的![]() 和
和![]() 浓度(单位:
浓度(单位:![]() ),得下表:
),得下表:
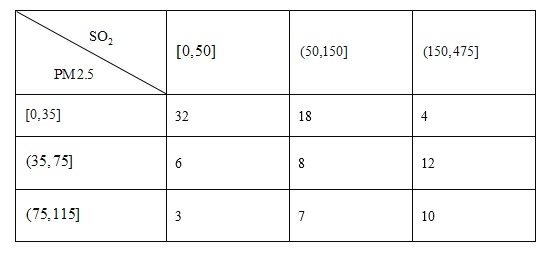
(1)估计事件“该市一天空气中![]() 浓度不超过
浓度不超过![]() ,且
,且![]() 浓度不超过
浓度不超过![]() ”的概率;
”的概率;
(2)根据所给数据,完成下面的![]() 列联表:
列联表:
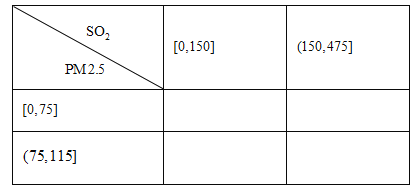
(3)根据(2)中的列联表,判断是否有![]() 的把握认为该市一天空气中
的把握认为该市一天空气中![]() 浓度与
浓度与![]() 浓度有关?
浓度有关?
附: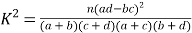 ,
,
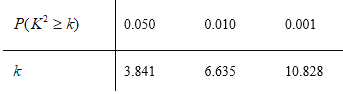
【答案】(1)![]() ;(2)答案见解析;(3)有.
;(2)答案见解析;(3)有.
【解析】
(1)根据表格中数据以及古典概型的概率公式可求得结果;
(2)根据表格中数据可得![]() 列联表;
列联表;
(3)计算出![]() ,结合临界值表可得结论.
,结合临界值表可得结论.
(1)由表格可知,该市100天中,空气中的![]() 浓度不超过75,且
浓度不超过75,且![]() 浓度不超过150的天数有
浓度不超过150的天数有![]() 天,
天,
所以该市一天中,空气中的![]() 浓度不超过75,且
浓度不超过75,且![]() 浓度不超过150的概率为
浓度不超过150的概率为![]() ;
;
(2)由所给数据,可得![]() 列联表为:
列联表为:
|
|
| 合计 |
| 64 | 16 | 80 |
| 10 | 10 | 20 |
合计 | 74 | 26 | 100 |
(3)根据![]() 列联表中的数据可得
列联表中的数据可得
![]()
![]() ,
,
因为根据临界值表可知,有![]() 的把握认为该市一天空气中
的把握认为该市一天空气中![]() 浓度与
浓度与![]() 浓度有关.
浓度有关.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目