题目内容
【题目】已知抛物线C的顶点为坐标原点O,对称轴为![]() 轴,其准线为
轴,其准线为![]() .
.
(1)求抛物线C的方程;
(2)设直线![]() ,对任意的
,对任意的![]() 抛物线C上都存在四个点到直线l的距离为
抛物线C上都存在四个点到直线l的距离为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据准线方程形式设抛物线标准方程,再根据数值求得![]() ,即得抛物线方程;
,即得抛物线方程;
(2)先根据![]() 确定
确定![]() ,再借助切线转化条件,即
,再借助切线转化条件,即![]() ,点
,点![]() 到抛物线
到抛物线![]() 切线
切线![]() 距离大于4恒成立,最后根据二次方程实根分布列不等式解得结果.
距离大于4恒成立,最后根据二次方程实根分布列不等式解得结果.
(1)由题意可设抛物线C的方程:![]() ,则
,则![]() 得
得![]() ,所以
,所以![]()
(2)由对任意的![]() 抛物线C上都存在四个点到直线l的距离为
抛物线C上都存在四个点到直线l的距离为![]() ,得
,得![]() ,
,
设与直线![]() 平行的直线
平行的直线![]() ,要满足题设条件“对任意的
,要满足题设条件“对任意的![]() 抛物线C上都有四个点到直线l的距离为
抛物线C上都有四个点到直线l的距离为![]() ”,
”,
则有当![]() 与抛物线
与抛物线![]() 相切时,
相切时,![]() 点
点![]() 到
到![]() 距离大于4恒成立,
距离大于4恒成立,
由![]() 得:
得:![]()
![]() 得
得![]()
点![]() 到
到![]() 距离为
距离为![]()
所以![]() 不等式
不等式![]() 恒成立,
恒成立,
代入![]() 整理得:
整理得:![]() ,令
,令![]() ,
,
即![]() 在
在![]() 上恒成立
上恒成立
所以①![]() 得
得![]() ,求得
,求得![]()
或②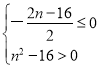 得
得![]()
所以![]()

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目