题目内容
如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=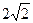 ,M为BC的中点
,M为BC的中点
(Ⅰ)证明:AM⊥PM ;
(Ⅱ)求二面角P-AM-D的大小;
(Ⅲ)求点D到平面AMP的距离
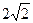 ,M为BC的中点
,M为BC的中点(Ⅰ)证明:AM⊥PM ;
(Ⅱ)求二面角P-AM-D的大小;
(Ⅲ)求点D到平面AMP的距离
(Ⅰ)证明见解析(Ⅱ)45°(Ⅲ)

(Ⅰ) 取CD的中点E,连结PE、EM、EA.
∵△PCD为正三角形,∴PE⊥CD,PE=PDsin∠PDE=2sin60°=
∵平面PCD⊥平面ABCD, ∴PE⊥平面ABCD (2分)
∵四边形ABCD是矩形
 ∴△ADE、△ECM、△ABM均为直角三角形
∴△ADE、△ECM、△ABM均为直角三角形
由勾股定理可求得:EM= ,AM=
,AM= ,AE=3
,AE=3
∴ (4分)
(4分)
 ,又
,又 在平面ABCD上射影:
在平面ABCD上射影:
∴∠AME=90°, ∴AM⊥PM (6分)
(Ⅱ)由(Ⅰ)可知EM⊥AM,PM⊥AM
∴∠PME是二面角P-AM-D的平面角 (8分)
∴tan ∠PME=
∴∠PME=45°
∴二面角P-AM-D为45°; (10分)
(Ⅲ)设D点到平面PAM的距离为 ,连结DM,则
,连结DM,则
 , ∴
, ∴
而 (12分)
(12分)
在 中,由勾股定理可求得PM=
中,由勾股定理可求得PM=
 ,所以:
,所以: ∴
∴
即点D到平面PAM的距离为 (14分)
(14分)
 解法2:(Ⅰ) 以D点为原点,分别以直线DA、DC为x轴、y轴,建立如图所示的空间直角坐标系
解法2:(Ⅰ) 以D点为原点,分别以直线DA、DC为x轴、y轴,建立如图所示的空间直角坐标系 ,
,
依题意,可得

 ……2分
……2分
∴
 (4分)
(4分)
∴
即 ,∴AM⊥PM (6分)
,∴AM⊥PM (6分)
(Ⅱ)设 ,且
,且 平面PAM,则
平面PAM,则
 即
即
∴ ,
, 
取 ,得
,得 (8分)
(8分)
取 ,显然
,显然 平面ABCD, ∴
平面ABCD, ∴
结合图形可知,二面角P-AM-D为45°; (10分)
(Ⅲ) 设点D到平面PAM的距离为 ,由(Ⅱ)可知
,由(Ⅱ)可知 与平面PAM垂直,则
与平面PAM垂直,则
 =
=
即点D到平面PAM的距离为 (14分)
(14分)
∵△PCD为正三角形,∴PE⊥CD,PE=PDsin∠PDE=2sin60°=

∵平面PCD⊥平面ABCD, ∴PE⊥平面ABCD (2分)
∵四边形ABCD是矩形
 ∴△ADE、△ECM、△ABM均为直角三角形
∴△ADE、△ECM、△ABM均为直角三角形由勾股定理可求得:EM=
 ,AM=
,AM= ,AE=3
,AE=3∴
 (4分)
(4分) ,又
,又 在平面ABCD上射影:
在平面ABCD上射影:∴∠AME=90°, ∴AM⊥PM (6分)
(Ⅱ)由(Ⅰ)可知EM⊥AM,PM⊥AM
∴∠PME是二面角P-AM-D的平面角 (8分)
∴tan ∠PME=

∴∠PME=45°
∴二面角P-AM-D为45°; (10分)
(Ⅲ)设D点到平面PAM的距离为
 ,连结DM,则
,连结DM,则 , ∴
, ∴
而
 (12分)
(12分)在
 中,由勾股定理可求得PM=
中,由勾股定理可求得PM=
 ,所以:
,所以: ∴
∴
即点D到平面PAM的距离为
 (14分)
(14分) 解法2:(Ⅰ) 以D点为原点,分别以直线DA、DC为x轴、y轴,建立如图所示的空间直角坐标系
解法2:(Ⅰ) 以D点为原点,分别以直线DA、DC为x轴、y轴,建立如图所示的空间直角坐标系 ,
,依题意,可得

 ……2分
……2分∴

 (4分)
(4分)∴

即
 ,∴AM⊥PM (6分)
,∴AM⊥PM (6分)(Ⅱ)设
 ,且
,且 平面PAM,则
平面PAM,则 即
即
∴
 ,
, 
取
 ,得
,得 (8分)
(8分)取
 ,显然
,显然 平面ABCD, ∴
平面ABCD, ∴
结合图形可知,二面角P-AM-D为45°; (10分)
(Ⅲ) 设点D到平面PAM的距离为
 ,由(Ⅱ)可知
,由(Ⅱ)可知 与平面PAM垂直,则
与平面PAM垂直,则 =
=
即点D到平面PAM的距离为
 (14分)
(14分)
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
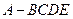 中,底面
中,底面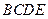 为矩形,侧面
为矩形,侧面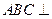 底面
底面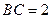 ,
,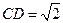 ,
,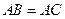 。
。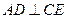 ;
;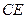 与平面
与平面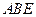 所成的角为
所成的角为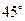 ,求二面角
,求二面角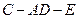 的大小。
的大小。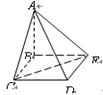
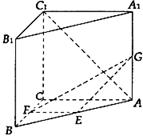
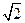 ,AC=3,BC=
,AC=3,BC=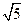 ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。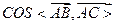 的值
的值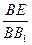 的值,不存在则说明理由。
的值,不存在则说明理由。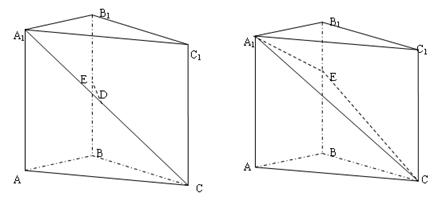
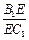 的值为多少时,
的值为多少时,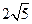 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交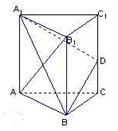
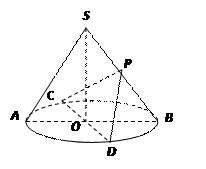
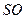 中,
中,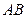 、
、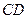 为底面圆的两条直径,
为底面圆的两条直径,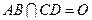 ,且
,且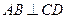 ,
,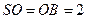 ,
,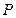 为
为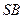 的中点.
的中点. 与
与 所成角的正切值.
所成角的正切值.