题目内容
在△ABC中,已知b=3,c=5,且C为钝角,则a的取值范围是( )A.(2,3)
B.(2,4)
C.(3,4)
D.(3,5)
【答案】分析:由余弦定理可得 cosC=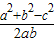 <0,故有 a2+b2-c2<0,解得a<4.再由任意两边之和大于第三边可得a>2.综合可得a的范围.
<0,故有 a2+b2-c2<0,解得a<4.再由任意两边之和大于第三边可得a>2.综合可得a的范围.
解答:解:由余弦定理可得 cosC=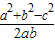 <0,∴a2+b2-c2<0,即 a2+9-25<0,解得a<4.
<0,∴a2+b2-c2<0,即 a2+9-25<0,解得a<4.
再由任意两边之和大于第三边可得 a+3>5,故a>2.
综上可得,2<a<4,
故选B.
点评:本题主要考查余弦定理,钝角的余弦值的符号以及三角形任意两边之和大于第三边,属于中档题.
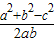 <0,故有 a2+b2-c2<0,解得a<4.再由任意两边之和大于第三边可得a>2.综合可得a的范围.
<0,故有 a2+b2-c2<0,解得a<4.再由任意两边之和大于第三边可得a>2.综合可得a的范围.解答:解:由余弦定理可得 cosC=
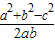 <0,∴a2+b2-c2<0,即 a2+9-25<0,解得a<4.
<0,∴a2+b2-c2<0,即 a2+9-25<0,解得a<4.再由任意两边之和大于第三边可得 a+3>5,故a>2.
综上可得,2<a<4,
故选B.
点评:本题主要考查余弦定理,钝角的余弦值的符号以及三角形任意两边之和大于第三边,属于中档题.

练习册系列答案
相关题目
 在△ABC中,已知B=45°,D是BC上一点,AD=5,AC=7,DC=3,求AB的长.
在△ABC中,已知B=45°,D是BC上一点,AD=5,AC=7,DC=3,求AB的长. 如图,在△ABC中,已知B=
如图,在△ABC中,已知B=