题目内容
已知函数g(x)=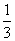 ax3+2x2-2x,函数f(x)是函数
ax3+2x2-2x,函数f(x)是函数 g(x)的导函数.
g(x)的导函数.
(1)若a=1,求g(x)的单调减区间;
(2)若对任意x1,x2∈R且x1≠x2,都有f ,求实数a的取值范围.
,求实数a的取值范围.
解析:(1)当a=1时,g(x)=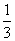 x3+2x2-2x,g′(x)=x2+4x-2,
x3+2x2-2x,g′(x)=x2+4x-2,
由g′(x)<0解得-2- <x<-2+
<x<-2+ .
.
∴当a=1时函数g(x)的单调减区间为 (-2- ,-2+
,-2+ );
);
(2)易知f(x)=g′(x)=ax2+4x-2,
依题意知f -
- =a
=a 2+4×
2+4× -2-
-2- =-
=- (x1-x2
(x1-x2 )2<0,
)2<0,
因为x1≠x2,所以a>0,即实数a的取值范围是(0,+∞).

练习册系列答案
相关题目
给出如下图所示程序,如果x1=2,x2=3,那么执行此程序的结果是输出( )
|

A.7 B.10 C.5 D.8
 x3-(1+a)x2+4ax+24a,其中常数a>1,则f(x) 的单调减区间为________.
x3-(1+a)x2+4ax+24a,其中常数a>1,则f(x) 的单调减区间为________. +ln x对任意x∈
+ln x对任意x∈ 恒成立,则a的最大值为( )
恒成立,则a的最大值为( )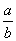 B.
B.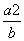 C.
C.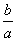 D.
D.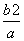
 x2
x2 x2 D.y=
x2 D.y= x2
x2 m](m>0)的最大值为-3,最小值为-4,则实数m的取值范围是( )
m](m>0)的最大值为-3,最小值为-4,则实数m的取值范围是( )